题目内容
已知⊙O的直径为10,AB是⊙O的一条直径,长为20的线段MN的中点P在⊙O上运动(异于A、B两点)。
(Ⅰ)求证: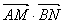 与点P在⊙O上的位置无关;
与点P在⊙O上的位置无关;
(Ⅱ)当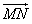 与
与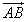 的夹角
的夹角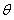 取何值时,
取何值时,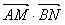 有最大值。
有最大值。
(Ⅰ)求证:
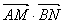 与点P在⊙O上的位置无关;
与点P在⊙O上的位置无关; (Ⅱ)当
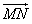 与
与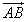 的夹角
的夹角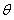 取何值时,
取何值时,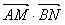 有最大值。
有最大值。 解:(Ⅰ)∵AB是⊙O的一条直径,P为圆上一点,
∴AP⊥BP,即 ⊥
⊥ ,
,
∴ ·
· =0,
=0,
∵P为MN中点,| |=20,
|=20,
∴ =
= ,|
,| |=|
|=| |=10,
|=10,
∴ =(
=( +
+ )·(
)·( +
+ )
)
=( -
- )·(
)·( +
+ )
)
= ·
· +
+ ·
· -
- ·
· -
- 2
2
= (
( -
- )-100
)-100
= ·
· -100=
-100=
 ·
· -100,
-100,
∴ 仅与
仅与 与
与 的夹角有关,而与点P位置无关。
的夹角有关,而与点P位置无关。
(Ⅱ)由(Ⅰ)有,
 =100cos
=100cos -100(0°≤
-100(0°≤ ≤180°),
≤180°),
∴当 =0°时,
=0°时, 取最大值0。
取最大值0。
∴AP⊥BP,即
 ⊥
⊥ ,
,∴
 ·
· =0,
=0,∵P为MN中点,|
 |=20,
|=20, ∴
 =
= ,|
,| |=|
|=| |=10,
|=10,∴
 =(
=( +
+ )·(
)·( +
+ )
)=(
 -
- )·(
)·( +
+ )
)=
 ·
· +
+ ·
· -
- ·
· -
- 2
2=
 (
( -
- )-100
)-100=
 ·
· -100=
-100=
 ·
· -100,
-100, ∴
 仅与
仅与 与
与 的夹角有关,而与点P位置无关。
的夹角有关,而与点P位置无关。(Ⅱ)由(Ⅰ)有,
 =100cos
=100cos -100(0°≤
-100(0°≤ ≤180°),
≤180°), ∴当
 =0°时,
=0°时, 取最大值0。
取最大值0。 
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 •
•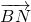 与点P在⊙O上的位置无关;
与点P在⊙O上的位置无关; 与
与 的夹角θ取何值时,
的夹角θ取何值时, •
•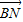 与点P在⊙O上的位置无关;
与点P在⊙O上的位置无关;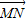 与
与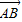 的夹角θ取何值时,
的夹角θ取何值时,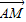 •
•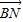 有最大值.
有最大值.