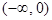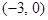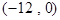题目内容
与抛物线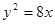 相切倾斜角为
相切倾斜角为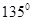 的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线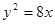 的准线所得的弦长为
的准线所得的弦长为
A.4 B.2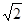 C.2 D.
C.2 D.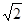
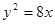 相切倾斜角为
相切倾斜角为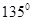 的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线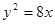 的准线所得的弦长为
的准线所得的弦长为A.4 B.2
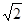 C.2 D.
C.2 D.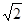
C
试题分析:
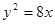 的准线方程为,x=-2设切线方程为
的准线方程为,x=-2设切线方程为 ,代入
,代入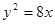 整理得,
整理得, ,则
,则 ,所以b=-2,切线方程为
,所以b=-2,切线方程为 ,A(-2,0),B(0,-2),过A、B两点的最小圆即以AB为直径的圆,所以截抛物线
,A(-2,0),B(0,-2),过A、B两点的最小圆即以AB为直径的圆,所以截抛物线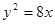 的准线所得的弦长为2.选C。
的准线所得的弦长为2.选C。点评:中档题,由于直线与抛物线相切,因此,两方程联立后所得一元二次方程根的判别式为0,从而可得切线方程。认识到过A、B两点的最小圆即以AB为直径的圆,是又一关键点。

练习册系列答案
相关题目
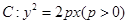 的焦点为
的焦点为 ,经过点
,经过点 交抛物线
交抛物线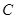 于点
于点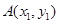 ,
,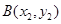 且
且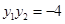 .
.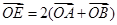 (
(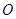 为坐标原点),且点
为坐标原点),且点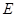 在抛物线
在抛物线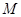 是抛物线
是抛物线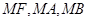 的斜率分别为
的斜率分别为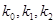 .求证:
.求证: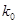 为定值时,
为定值时,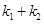 也为定值.
也为定值.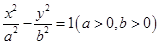 的左焦点
的左焦点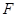 引圆
引圆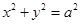 的切线,切点为
的切线,切点为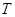 ,延长
,延长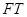 交双曲线右支于
交双曲线右支于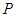 点,若
点,若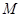 为线段
为线段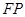 的中点,
的中点, 为坐标原点,则
为坐标原点,则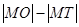 与
与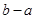 的大小关系为( )
的大小关系为( )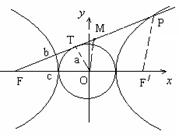
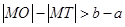
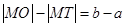
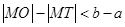
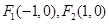 为椭圆
为椭圆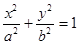 的两个焦点,若椭圆上一点
的两个焦点,若椭圆上一点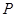 满足
满足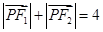 ,则椭圆的离心率
,则椭圆的离心率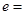 ( )
( )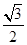
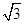
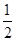

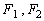 为双曲线
为双曲线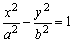 的左右焦点,点P在双曲线上,
的左右焦点,点P在双曲线上, 的平分线分线段
的平分线分线段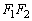 的比为5∶1,则双曲线的离心率的取值范围是 .
的比为5∶1,则双曲线的离心率的取值范围是 .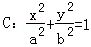 的右焦点F,抛物线:
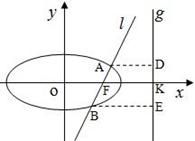
的右焦点F,抛物线: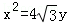 的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且
的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且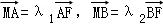 ,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点
,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点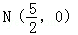 .
.
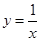 的图象为双曲线,在双曲线的两支上分别取点
的图象为双曲线,在双曲线的两支上分别取点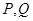 ,则线段
,则线段 的最小值为 ;
的最小值为 ; 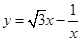 的图象为双曲线,在此双曲线的两支上分别取点
的图象为双曲线,在此双曲线的两支上分别取点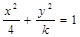 的离心率
的离心率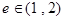 ,则k的取值范围是( )
,则k的取值范围是( )