题目内容
一个口袋中装有2个白球和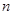 个红球(
个红球(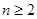 且
且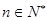 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(Ⅰ) 摸球一次,若中奖概率为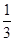 ,求
,求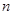 的值;
的值;
(Ⅱ) 若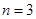 ,摸球三次,记中奖的次数为
,摸球三次,记中奖的次数为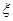 ,试写出
,试写出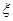 的分布列并求其期望.
的分布列并求其期望.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)由古典概率的求法,可求出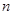 ;(Ⅱ)摸球三次,中奖情况可能为;0,1,2,3次,分别求出概率,得分布列从而求出期望.
;(Ⅱ)摸球三次,中奖情况可能为;0,1,2,3次,分别求出概率,得分布列从而求出期望.
试题解析:(1) ;
;
(2)若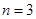 ,则每次摸球中奖的概率
,则每次摸球中奖的概率
因此, ,分布列如下:
,分布列如下: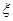
0 1 2 3 P 



 .
.
考点:1、古典概率的求法,2、分布列与期望的求法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排列组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
(1)求
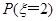 ;
;(2)求随机变量
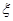 的分布列和数学期望.
的分布列和数学期望. 为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示:
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
| 组别 | 候车时间 | 人数 |
| 一 | 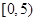 | 2 |
| 二 | 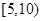 | 6 |
| 三 | 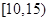 | 4 |
| 四 | 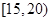 | 2 |
| 五 | 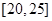 | 1 |
(本小题满分12分)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
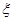 表示密码中不同数字的个数.
表示密码中不同数字的个数.(Ⅰ)求
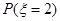 ; (Ⅱ)求随机变量
; (Ⅱ)求随机变量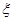 的分布列和它的数学期望.
的分布列和它的数学期望. 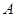 到
到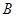 有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为
有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为 .
.
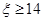 时,线路信息畅通,求线路信息畅通的概率;
时,线路信息畅通,求线路信息畅通的概率; ,记政治、历史、地理达到优秀水平的事件分别为
,记政治、历史、地理达到优秀水平的事件分别为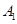 、
、 、
、 ,未达到优秀水平的事件分别为
,未达到优秀水平的事件分别为 、
、 、
、 .
. ,试求事件
,试求事件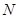 ,使得事件
,使得事件 ,并说明理由.
,并说明理由. 和获得等级不是
和获得等级不是 、
、 、
、 ,物理、化学、生物获得等级不是
,物理、化学、生物获得等级不是 、
、 、
、 .
. );
);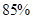 ,并说明理由.
,并说明理由.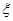 ,求
,求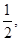 各局比赛的结果都相互独立,第
各局比赛的结果都相互独立,第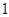 局甲当裁判.
局甲当裁判. 局甲当裁判的概率;
局甲当裁判的概率;