Question

 

已知函数对任意实数x均有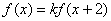，其中常数k为负数，且在区间[0，2]上有表达式

   （1）求的值；

   （2）写出在[－3，3]上的表达式，并讨论函数在[－3，3]上的单调性；

   （3）求出在[－3，3]上的最小值与最大值，并求出相应的自变量的取值.

  

 

 

Answer 1

【答案】

 解：由于

    当

   （1）

   （2）当时，

当时，

当时，

f(x)=

    

    

由于k为负数，易画出在[—3，3]的图形。

由图形可知：[—3，—1]为单调增区间；

[—1，1]为单调减区间；

[1，3]为单调增区间

   （3）由（2）可知，

a．当

此时：

b．当

此时：

c．当时，

此时：