题目内容
已知函数![]() 对任意实数x、y都有
对任意实数x、y都有![]() =
=![]() ·
·![]() ,且
,且![]() ,
,![]() ,当
,当![]() 时,0≤
时,0≤![]() <1.
<1.
(1)求![]() 及
及![]() 的值;
的值;
(2)判断![]() 的奇偶性;
的奇偶性;
(3)判断![]() 在[0,+∞
在[0,+∞![]() 上的单调性,并给出证明;
上的单调性,并给出证明;
(4)若![]() 且
且![]() ≤
≤![]() ,求
,求![]() 的取值范围.
的取值范围.
解:⑴![]() =0 ……………1分
=0 ……………1分
∵![]() =9,又
=9,又![]() =
=![]() ·
·![]() =
=![]() ·
·![]() ·
·![]() = [
= [![]() ]
]![]() ,
,
∴9 = [![]() ]
]![]() ,∴
,∴![]() =
=![]() ,……………3分
,……………3分
⑵令y =-1,则![]() =
=![]() ·
·![]() ,
,
∵![]() =1,∴
=1,∴![]() =
= ![]() ,且
,且![]() 所以
所以![]() 为偶函数.……………6分
为偶函数.……………6分
⑶若x≥0,则![]() =
=![]() =
=![]() ·
·![]() =[
=[![]() ]
]![]() ≥0.……………7分
≥0.……………7分
若存在![]() ,则
,则![]() ,矛盾,
,矛盾,
所以当![]() 时,
时,![]() ……………8分
……………8分
设0≤x![]() <x
<x![]() ,则0≤
,则0≤![]() <1,∴
<1,∴![]() =
=![]() =
=![]() ·
·![]() ,……………9分
,……………9分
∵当x≥0时![]() ≥0,且当0≤x<1时,0≤
≥0,且当0≤x<1时,0≤![]() <1.
<1.
∴0≤![]() <1,∴
<1,∴![]() <
<![]() ,故函数
,故函数![]() 在[0,+∞
在[0,+∞![]() 上是增函数.………11分
上是增函数.………11分
(4)∵![]() ≤
≤![]() ,∴
,∴![]() ≤
≤![]() ,……………12分
,……………12分
∵a≥0,(a+1),3![]() [0,+∞
[0,+∞![]() ,函数在[0,+∞
,函数在[0,+∞![]() 上是增函数.
上是增函数.
∴a+1≤3,即a≤2, ……………13分
又a≥0,故0≤a≤2.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 对任意实数x,函数值恒大于0,求实数k的取值范围.
对任意实数x,函数值恒大于0,求实数k的取值范围. 对任意实数x,函数值恒大于0,求实数m的取值范围.
对任意实数x,函数值恒大于0,求实数m的取值范围. 对任意实数x均有
对任意实数x均有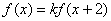 ,其中常数k为负数,且
,其中常数k为负数,且
 的值;
的值;