题目内容
已知A是由实数组成的数集,满足:a∈A则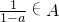 ;且1∉A.
;且1∉A.
(1)若2∈A,则A中至少含有哪些元素;
(2)A能否为单元素集合?若能,求出集合A;若不能,说明理由;
(3)若a∈A,则 是A中的元素吗?说明理由.
是A中的元素吗?说明理由.
解:(1)2∈A得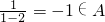 ,
,
得 ,
,
得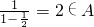 ,
,
所以, ….4分
….4分
(2)设A={a},则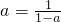 ,即a2-a+1=0,该方程无实数解…8分
,即a2-a+1=0,该方程无实数解…8分
(3)由1∉A知a≠0,∴
得 ,
,
所以 是A中元素 …..11分.
是A中元素 …..11分.
分析:(1)根据集合A的元素的性质知,a与 都在集合A中,故由2∈A,在利用
都在集合A中,故由2∈A,在利用  进行求解,直到求出三个元素为止,用列举法表示出来;
进行求解,直到求出三个元素为止,用列举法表示出来;
(2)由a与 都在集合A中,再由集合A只含有一个元素得,故假设a∈A时,有a=
都在集合A中,再由集合A只含有一个元素得,故假设a∈A时,有a= 进行求解,若有解则存在,若无解则不存在.
进行求解,若有解则存在,若无解则不存在.
(3)由1∉A知a≠0,∴得出 ,进一步得到得
,进一步得到得  ,从而得出结论.
,从而得出结论.
点评:本题考查了元素与集合的关系,主要根据集合元素的特征进行求解,对于存在型的问题,需要先假设存在有条件列出方程进行求解说明,考查了逻辑思维能力.
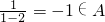 ,
,得
 ,
,得
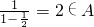 ,
,所以,
 ….4分
….4分(2)设A={a},则
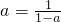 ,即a2-a+1=0,该方程无实数解…8分
,即a2-a+1=0,该方程无实数解…8分(3)由1∉A知a≠0,∴

得
 ,
,所以
 是A中元素 …..11分.
是A中元素 …..11分.分析:(1)根据集合A的元素的性质知,a与
 都在集合A中,故由2∈A,在利用
都在集合A中,故由2∈A,在利用  进行求解,直到求出三个元素为止,用列举法表示出来;
进行求解,直到求出三个元素为止,用列举法表示出来;(2)由a与
 都在集合A中,再由集合A只含有一个元素得,故假设a∈A时,有a=
都在集合A中,再由集合A只含有一个元素得,故假设a∈A时,有a= 进行求解,若有解则存在,若无解则不存在.
进行求解,若有解则存在,若无解则不存在.(3)由1∉A知a≠0,∴得出
 ,进一步得到得
,进一步得到得  ,从而得出结论.
,从而得出结论.点评:本题考查了元素与集合的关系,主要根据集合元素的特征进行求解,对于存在型的问题,需要先假设存在有条件列出方程进行求解说明,考查了逻辑思维能力.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目