题目内容
(本小题满分12分)
已知函数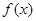 的定义域是
的定义域是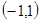 ,对于任意的
,对于任意的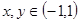 ,有
,有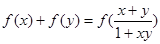 ,且当
,且当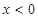 时,
时,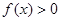 .
.
(Ⅰ)验证函数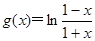 是否满足上述这些条件;
是否满足上述这些条件;
(Ⅱ)你发现这样的函数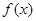 还具有其它什么样的主要性质?试就函数的奇偶性、单调性的结论写出来,并加以证明.
还具有其它什么样的主要性质?试就函数的奇偶性、单调性的结论写出来,并加以证明.
已知函数
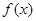 的定义域是
的定义域是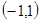 ,对于任意的
,对于任意的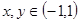 ,有
,有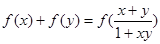 ,且当
,且当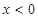 时,
时,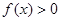 .
.(Ⅰ)验证函数
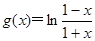 是否满足上述这些条件;
是否满足上述这些条件;(Ⅱ)你发现这样的函数
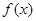 还具有其它什么样的主要性质?试就函数的奇偶性、单调性的结论写出来,并加以证明.
还具有其它什么样的主要性质?试就函数的奇偶性、单调性的结论写出来,并加以证明.解:(Ⅰ)由
 ,即其定义域为
,即其定义域为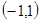 ;………………………… 2分
;………………………… 2分又

 ,
, ,
,有
 成立;……………………………………………………… 4分
成立;……………………………………………………… 4分又当
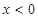 时,
时, ,∴
,∴  ,有
,有 成立;
成立;∴ 综上:
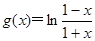 满足这些条件.……………………………………………… 6分
满足这些条件.……………………………………………… 6分(Ⅱ)发现这样的函数
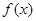 在
在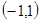 上是奇函数.…………………………………………7分
上是奇函数.…………………………………………7分∵
 代入条件得,
代入条件得, ,
,∵
 代入条件得,
代入条件得, ,
,∴ 函数
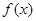 在
在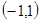 上是奇函数. …………………………………………………9分
上是奇函数. …………………………………………………9分又发现这样的函数
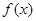 在
在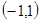 上是减函数. …………………………………………10分
上是减函数. …………………………………………10分∵
 ,
,当
 时,
时, ,由条件知
,由条件知 ,
,即
 ,
,∴ 函数
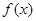 在
在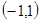 上是减函数.……………………………………………………12分
上是减函数.……………………………………………………12分略

练习册系列答案
相关题目
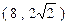 ,求出函数解析式,并指出函数的单调性与奇偶性。
,求出函数解析式,并指出函数的单调性与奇偶性。 在点(2, 4)处的切线方程是( )
在点(2, 4)处的切线方程是( )



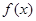 是定义在
是定义在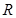 上不恒为
上不恒为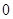 的函数,且对于任意的实数
的函数,且对于任意的实数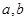 满足
满足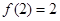 ,
,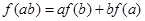 ,
,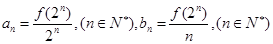 ,考察下列结论:①
,考察下列结论:①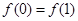 ②
②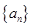 为等差数列 ④数列
为等差数列 ④数列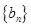 为等比数列,其中正确的个数为( )
为等比数列,其中正确的个数为( )



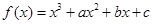 ,曲线
,曲线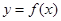 在
在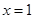 处的切线方程为
处的切线方程为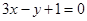 ,若
,若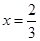 时,
时, 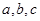 的值; (2)求
的值; (2)求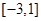 上的最大值和最小值.
上的最大值和最小值. 在点(1,
在点(1, )处的切线与直线
)处的切线与直线 平行,则
平行,则 ( )
( )



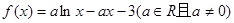
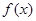 的单调区间;
的单调区间;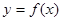 的图像在点
的图像在点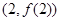 处的切线的斜率为
处的切线的斜率为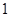 ,问:
,问: 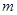 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的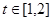 ,函数
,函数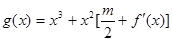 在区间
在区间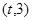 上总存在极值?
上总存在极值?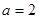 时,设函数
时,设函数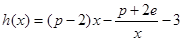 ,若在区间
,若在区间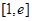 上至少存在一个
上至少存在一个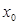 ,使得
,使得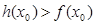 成立,试求实数
成立,试求实数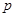 的取值范围.
的取值范围.
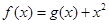 ,曲线
,曲线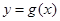 在点
在点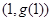 处的切线方程为
处的切线方程为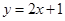 ,则曲线
,则曲线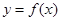 在点
在点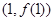 处切线的斜率为 ( )
处切线的斜率为 ( )