题目内容
(本小题14分)已知函数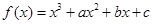 ,曲线
,曲线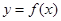 在
在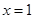 处的切线方程为
处的切线方程为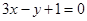 ,若
,若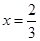 时,
时, 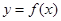 有极值.
有极值.
(1)求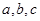 的值; (2)求
的值; (2)求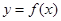 在区间
在区间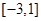 上的最大值和最小值.
上的最大值和最小值.
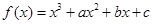 ,曲线
,曲线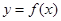 在
在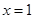 处的切线方程为
处的切线方程为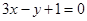 ,若
,若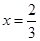 时,
时, 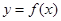 有极值.
有极值.(1)求
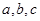 的值; (2)求
的值; (2)求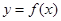 在区间
在区间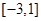 上的最大值和最小值.
上的最大值和最小值.解: (1)由f(x)=x3+ax2+bx+c,
得f′(x)=3x2+2ax+b,
当x=1时,切线l的斜率为3,可得2a+b="0 " ①
当x=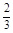 时,y=f(x)有极值,则f′(
时,y=f(x)有极值,则f′(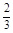 )=0,
)=0,
可得4a+3b+4="0 " ②
由①②解得a=2,b=-4.
由于切点的横坐标为x=1,∴f(1)=4.
∴1+a+b+c=4.∴c=5………………………………….6分
(2)由(1)可得f(x)=x3+2x2-4x+5,
∴f′(x)=3x2+4x-4,
令f′(x)=0,得x=-2,x=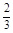 .
.
当x变化时,y,y′的取值及变化如下表:
∴ y=f(x)在[-3,1]上的最大值为13,最小值为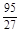 …………………….14分
…………………….14分
得f′(x)=3x2+2ax+b,
当x=1时,切线l的斜率为3,可得2a+b="0 " ①
当x=
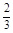 时,y=f(x)有极值,则f′(
时,y=f(x)有极值,则f′(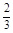 )=0,
)=0,可得4a+3b+4="0 " ②
由①②解得a=2,b=-4.
由于切点的横坐标为x=1,∴f(1)=4.
∴1+a+b+c=4.∴c=5………………………………….6分
(2)由(1)可得f(x)=x3+2x2-4x+5,
∴f′(x)=3x2+4x-4,
令f′(x)=0,得x=-2,x=
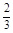 .
.当x变化时,y,y′的取值及变化如下表:
| x | -3 | (-3,-2) | -2 | (-2,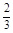 ) ) | 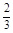 | (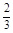 ,1) ,1) | 1 |
 | | + | 0 | - | 0 | + | |
| y | 8 |  单调增递 单调增递 | 13 |  单调递减 单调递减 | 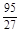 |  单调递增 单调递增 | 4 |
∴ y=f(x)在[-3,1]上的最大值为13,最小值为
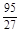 …………………….14分
…………………….14分略

练习册系列答案
相关题目

 是函数
是函数 的极值点,其中
的极值点,其中 是自然对数的底数。
是自然对数的底数。 同时满足:
同时满足: 处的切线 ,
处的切线 ,  的图象
的图象 相切于点
相切于点
 ,求实数b的取值范围
,求实数b的取值范围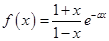

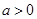 ,讨论
,讨论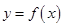 的单调性;
的单调性;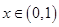 恒有
恒有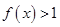 ,求
,求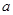 的取值范围
的取值范围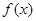 的定义域是
的定义域是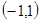 ,对于任意的
,对于任意的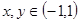 ,有
,有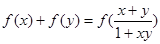 ,且当
,且当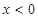 时,
时,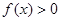 .
.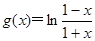 是否满足上述这些条件;
是否满足上述这些条件;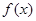 对
对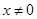 的任意实数,恒有
的任意实数,恒有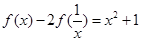 成立.
成立.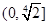 上是增函数
上是增函数 的图象与直线
的图象与直线 相切,则a等于( )
相切,则a等于( )


 的定义域是:
的定义域是:



 在
在 处的切线方程为 .
处的切线方程为 . 在
在 处有极值10,则
处有极值10,则 的值为 ( ▲ )
的值为 ( ▲ )

