题目内容
已知函数 .其中
.其中
(1)求函数的最大值和最小值
(2)若 ,求x0的值.
,求x0的值.
解:(1)当 在
在 上增,∴
上增,∴ ,
,
而当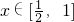 时,f(x)=-2x+2减,∴0≤f(x)≤1
时,f(x)=-2x+2减,∴0≤f(x)≤1
综上可得:f(x)的最大值为1,最小值为0;
(2) ,
,
由上得 ,∴f(x1)=-2x1+2=
,∴f(x1)=-2x1+2= ,
,
整理可得 ,解得
,解得 ,
,
由条件得 即为所求.
即为所求.
分析:(1)由分段函数的特点,分别代入可得取值范围,综合可得;
(2)由x0的范围,选择解析式可得x1,再由x1的范围可选解析式,代入可得x0的方程,解之即可.
点评:本题考查分段函数的最值问题,分段代入是解决问题的关键,属中档题.
 在
在 上增,∴
上增,∴ ,
,而当
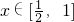 时,f(x)=-2x+2减,∴0≤f(x)≤1
时,f(x)=-2x+2减,∴0≤f(x)≤1综上可得:f(x)的最大值为1,最小值为0;
(2)
 ,
,由上得
 ,∴f(x1)=-2x1+2=
,∴f(x1)=-2x1+2= ,
,整理可得
 ,解得
,解得 ,
,由条件得
 即为所求.
即为所求.分析:(1)由分段函数的特点,分别代入可得取值范围,综合可得;
(2)由x0的范围,选择解析式可得x1,再由x1的范围可选解析式,代入可得x0的方程,解之即可.
点评:本题考查分段函数的最值问题,分段代入是解决问题的关键,属中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
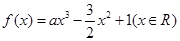 ,其中
,其中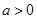 .
.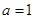 ,求曲线
,求曲线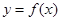 在点
在点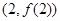 处的切线方程;
处的切线方程;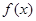 有三个零点,求
有三个零点,求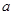 的取值范围.
的取值范围.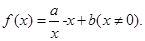 ,其中
,其中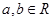
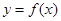 在点
在点 处的切线方程为
处的切线方程为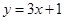 ,求函数
,求函数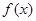 的解析式;
的解析式;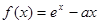 ,其中
,其中 .
. 恒成立,求
恒成立,求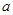 的取值范围;
的取值范围; 的图像上取定两点
的图像上取定两点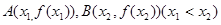 ,记直线
,记直线 的斜率为
的斜率为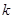 ,证明:存在
,证明:存在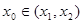 ,使
,使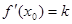 成立.
成立.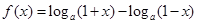 ,其中
,其中 .
.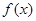 的定义域;
的定义域;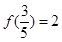 ,求使
,求使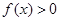 成立的
成立的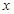 的集合。
的集合。