题目内容
已知函数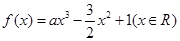 ,其中
,其中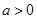 .
.
(1)若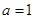 ,求曲线
,求曲线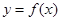 在点
在点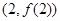 处的切线方程;
处的切线方程;
(2)求函数的极大值和极小值,若函数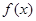 有三个零点,求
有三个零点,求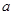 的取值范围.
的取值范围.
【答案】
(1)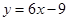 ;(2)
;(2)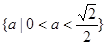 .
.
【解析】
试题分析:(1)本小题首先代入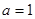 求得原函数的导数,然后求出切点坐标和切线的斜率,最后利用点斜式求得切线方程
求得原函数的导数,然后求出切点坐标和切线的斜率,最后利用点斜式求得切线方程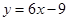 ;
;
(2)本小题首先求得原函数的导数,通过导数零点的分析得出原函数单调性,做成表格,求得函数的极大值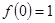 和极小值
和极小值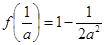 ,若要
,若要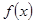 有三个零点,只需
有三个零点,只需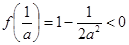
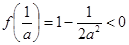 即可,解不等式即可.
即可,解不等式即可.
试题解析:(Ⅰ)当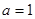 时,
时,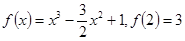 ;
;

所以曲线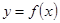 在点
在点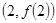 处的切线方程为
处的切线方程为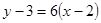 ,
,
即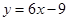 6分
6分
(Ⅱ)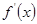 =
=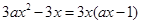 .令
.令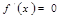 ,解得
,解得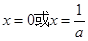 8分
8分
因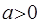 ,则
,则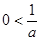 .当
.当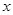 变化时,
变化时,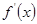 、
、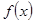 的变化情况如下表:
的变化情况如下表:
|
x |
|
0 |
|
|
|
|
f’(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
递增 |
极大值 |
递减 |
极小值 |
递增 |
则极大值为: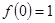 ,极小值为:
,极小值为: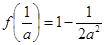 ,
,
若要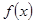 有三个零点,
有三个零点,
只需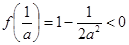 即可,
即可,
解得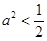 ,又
,又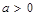 .因此
.因此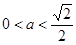
故所求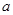 的取值范围为
的取值范围为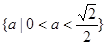 13分
13分
考点:1.用导数求切线方程;2.用导数分析函数的单调性、极值.

练习册系列答案
相关题目










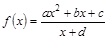 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.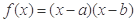 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
