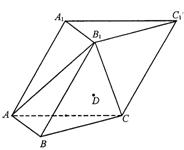
题目内容
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,点A1在底面ABC内的射影O恰为线段AC的中点.
(Ⅰ)求侧棱AA1与平面A1BC所成角的正弦值;
(Ⅱ)已知点D为点B关于点O的对称点,在直线AA1上是否存在点P,使DP∥平面AB1C?若存在,请确定点P的位置;若不存在,请说明理由.

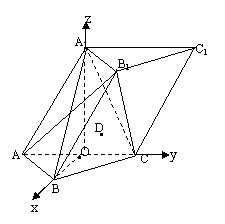
解:以O为坐标原点,DB,OC,OA1依次为![]() 轴、
轴、![]() 轴,
轴,![]() 轴正方向建立空间直角坐标系,则点A1(0,0,
轴正方向建立空间直角坐标系,则点A1(0,0,![]() ),A(0,-1,0),B(
),A(0,-1,0),B(![]() ,0,0),C(0,1,0)
,0,0),C(0,1,0)
(Ⅰ)![]() ,
,
设平面A1BC的一个法向量为![]()
则 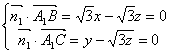
∴![]() =(
=(![]()
设直线AA1与平面A1BC所成角为θ
则 sinθ=|cos<![]() ,
,![]() >|=
>|=![]()
即侧棱AA1与平面A1BC所成角正弦值为![]() .
.
(Ⅱ)设B1(![]() ,则
,则![]()
∵![]()
∴![]() =
=![]() ∴
∴![]()
∴B1![]() ,
,
∴![]()
设平面ACB1的一个法向量是![]() ,
,
则![]()
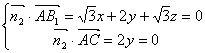
∴![]() =(-1,0,1)
=(-1,0,1)
假设在AA1上存在P(0,m,n)使DP∥平面AB1C,
∵D、B关于O对称 ∴D![]() ∴
∴![]() =(
=(![]() ,m,n)
,m,n)
∴![]()
![]() =
=![]() ∴n=
∴n=![]()
故当点P与A1重合时,DP∥平面AB1C.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
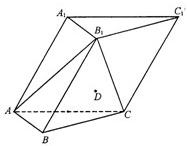 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°. B
B ,在直线AA
,在直线AA
 B
B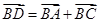 ,在直线AA
,在直线AA