题目内容

13．已知F1、F2为双曲线：$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{20}$=1的左、右焦点，过F2的直线交双曲线于A，B两点，则△F1AB周长的最小值为（　　）
A．8B．16C．20D．36

分析 根据双曲线的定义和性质，当弦AB垂直于x轴时，即可求出三角形的周长的最小值．

解答 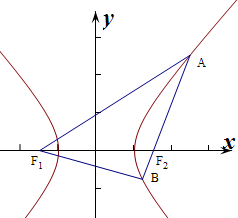解：由双曲线的方程可知a=4，
则|AF1|-|AF2|=2a=8，|BF1|-|BF2|=8，
则|AF1|+|BF1|-（|BF2|+|AF2|）=16，
即|AF1|+|BF1|=|BF2|+|AF2|+4=|AB|+16，
则当AB垂直于x轴时，周长取得最小值，
且为2|AB|+16=2•$\frac{2{b}^{2}}{a}$+16=2×$\frac{2×20}{4}$+16=36．
故选：D．

点评 本题主要考查双曲线的定义，根据双曲线的定义得到A，B到两焦点距离之差是个常数是解决本题的关键．

练习册系列答案
相关题目
3．已知函数f（x）=alnx-ax-3（a≠0）．
（1）讨论f（x）的单调性；
（2）若f（x）+（a+1）x+4-e≤0对任意x∈[e，e2]恒成立，求实数a的取值范围（e为自然常数）；
（3）求证：ln（$\frac{1}{2^2}$+1）+ln（$\frac{1}{3^2}$+1）+ln（$\frac{1}{4^2}$+1）+…+ln（$\frac{1}{n^2}$+1）＜1（n≥2，n∈N*）．
4．已知函数f（x）=2a•4x-2x-1．
（1）若a=1，求当x∈[-3，0]时，函数f（x）的取值范围；
（2）若关于x的方程f（x）=0有实数根，求实数a的取值范围．
1．在△ABC中，角A，B，C的对边分别为a，b，c，且$2bcosA-\sqrt{3}ccosA=\sqrt{3}acosC$．
（1）求角A的值；
（2）若$∠B=\frac{π}{6}$，BC边上中线$AM=\sqrt{7}$，求△ABC的面积．
8．设椭圆$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}$=1，则该椭圆的焦点坐标为（　　）
A．（-$\sqrt{5}$，0），（$\sqrt{5}$，0）B．（0，-$\sqrt{5}$），（0，$\sqrt{5}$）C．（-$\sqrt{13}$，0），（$\sqrt{13}$，0）D．（0，-$\sqrt{13}$），（0，$\sqrt{13}$）
18．已知椭圆的中心在坐标原点，焦点在x轴上，离心率为$\frac{1}{2}$，右焦点到左顶点的距离为3．
（1）、求椭圆的方程；
（2）、直线l过点E（-1，0）且与椭圆交于A，B两点，若$\overrightarrow{AE}$=2$\overrightarrow{EB}$，求直线l的方程．
5．已知△ABC中，AB=3，∠A=30°，∠B=120°，则△ABC的面积为$\frac{{9\sqrt{3}}}{4}$．
11．某几何体的三视图如图所示，则该几何体的表面积是（　　）
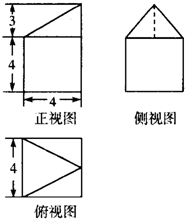
A．98+6$\sqrt{5}$B．106+6$\sqrt{5}$C．114+6$\sqrt{5}$D．106+12$\sqrt{5}$
12．田径场上正在进行100米决赛，参加决赛的是A、B、C、D、E、F六个人，小李、小张、小王对谁会取得冠军谈了自己的看法：小张认为，冠军不是A就是B；小王坚信，冠军决不是C；小李则认为，D、F都不可能取得冠军，比赛结束后，人们发现三个人中只有一个人的看法是错误的，则100米决赛的冠军是（　　）
A．AB．BC．CD．D

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网