Question

已知△ABC是边长为4的正三角形，D、P是△ABC内部的两点，且满足

AD

=

1

4

（

AB

+

AC

），

AP

=

AD

+

1

8

BC

，则△APD的面积是（　　）

• A、

  3

  6

• B、

  3

  4

• C、

  3

  3

• D、

  3

  3

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：以A为原点，以BC的垂直平分线为y轴，建立直角坐标系．由于等边三角形△的边长为4，可得B(-2，-2

3

)，C(2，-2

3

)，再利用向量的坐标运算和数乘运算可得

AD

，

AP

，利用△APD的面积S=

1

2

|

AD

|•|

DP

|即可得出．

解答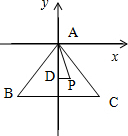： 解：以A为原点，以BC的垂直平分线为y轴，建立直角坐标系．
∵等边三角形△的边长为4，
∴B(-2，-2

3

)，C(2，-2

3

)
由

AD

=

1

4

（

AB

+

AC

）=

1

4

[(-2，-2

3

)+(2，-2

3

)]=(0，-

3

)，

AP

=

AD

+

1

8

BC

=(0，-

3

)+

1

8

(4，0)=(

1

2

，-

3

)，
∴△APD的面积S=

1

2

|

AD

|•|

DP

|=

1

2

×

3

×

1

2

=

3

4

．
故选：B．

点评：本题考查了向量的坐标运算和数乘运算、三角形的面积计算公式，属于中档题．