Question

如图,直线l过点A(2,3),并且被两平行线l₁:3x+4y-7=0和l₂:3x+4y+8=0截得的线段长为3,试求直线l的方程.

Answer 1

思路解析：由l被l₁、l₂截得线段长为3,又l₁、l₂间的距离为3,可求得l与l₂的夹角为45°,由夹角公式可求l的斜率,从而得解.

解：设直线l的方程为y-3=k(x-2),即kx-y+3-2k=0.

设l与l₁交于点M,作MN⊥l₂于点N(如图7-3-8).

两平行线l₁、l₂间距离|MN|==3.

在Rt△MNQ中,|MQ|=3,sin∠MQN==,∴∠MQN=45°,即直线l与l₂的夹角是45°.于是tan45°=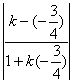.解之,得k=或k=-7.

∴所求直线方程为x-7y+19=0或7x+y-17=0.

深化升华

    本题构造一个Rt△MNQ,求l₂与l的夹角,进而求出所求直线的斜率,从而求出直线l的方程.本题如采用解方程组的方法求交点M(,),Q(,),再利用|MQ|=3来解出k,运算很繁杂,比较之下,本题用前一类解法好.