题目内容
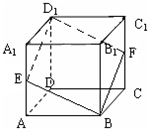如图，已知E、F分别是正方体ABCD-A1B1C1D1的棱AA1和棱CC1上的中点，求证：四边形EBFD1是菱形．
分析：根据菱形的定义直接证明即可．
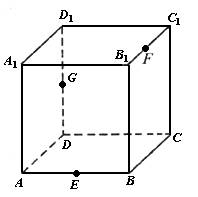
解答：证明：取棱BB1中点为G，连C1G、EG，
由正方体性质，侧面AB B1A1为正方形，
又E、G分别为边AA1、BB1中点，
所以 EG=A1B1=C1D1，EG∥A1B1∥C1D1，
从而四边形EGC1D1为平行四边形，
∴D1E∥C1G，D1E=C1G，
又F、G分别为棱CC1、BB1中点，
由侧面CB B1C1为正方形，知四边形BGC1F 为平行四边形，
所以BF∥C1G，BF=C1G，
又∴D1E∥C1G，D1E=C1G，
由平行公理可知D1E=BF，D1E∥BF，
从而四边形EBFD1 为平行四边形．
由ABCD-A1B1C1D1为正方体，不妨设其棱长为a，易
知 BE=BF=
a
而由四边形 EBFD1为平行四边形，从而即为菱形．
由正方体性质，侧面AB B1A1为正方形，
又E、G分别为边AA1、BB1中点，
所以 EG=A1B1=C1D1，EG∥A1B1∥C1D1，
从而四边形EGC1D1为平行四边形，
∴D1E∥C1G，D1E=C1G，
又F、G分别为棱CC1、BB1中点，
由侧面CB B1C1为正方形，知四边形BGC1F 为平行四边形，
所以BF∥C1G，BF=C1G，
又∴D1E∥C1G，D1E=C1G，
由平行公理可知D1E=BF，D1E∥BF，
从而四边形EBFD1 为平行四边形．
由ABCD-A1B1C1D1为正方体，不妨设其棱长为a，易
知 BE=BF=
| ||
| 2 |
而由四边形 EBFD1为平行四边形，从而即为菱形．
点评：本题主要考查菱形的判断和证明，利用平行的传递性是解决本题的关键．
练习册系列答案
相关题目
.