Question

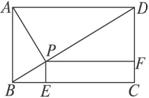
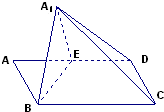在矩形ABCD中，AB：AD=1：2，E是AD的中点，沿BE将△ABE折起至△A₁BE的位置，使A₁C=A₁D．
（1）求证：面A₁BE⊥面BCDE；
（2）若BC=2，求A₁C与面A₁BE所成角的正切值．

Answer 1

分析：（1）作A₁F⊥BE于F，A₁G⊥CD于G，连FG，证明FG是梯形BCDE的中位线，进而证明CD⊥面A₁FG，A₁F⊥面BCDE，利用面面垂直的判定定理，可得面A₁BE⊥面BCDE；
（2）连接CE，证明CE⊥面A₁BE，可得∠CA₁E为A₁C与面A₁BE所成角，从而可求A₁C与面A₁BE所成角的正切值．

解答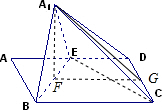：（1）证明：作A₁F⊥BE于F，A₁G⊥CD于G，连FG．
∵AB：AD=1：2，E是AD中点，
∴AB=AE，即A₁BA₁E．
∵A₁F⊥BE，
∴AF=FE，
∵A₁C=A₁D，A₁G⊥CD，
∴CG=GD，
∴FG是梯形BCDE的中位线，
∴BC∥FG∥DE，
∴FG⊥CD．
∵A₁G⊥CD，
∴CD⊥面A₁FG，
∴CD⊥A₁F．
∵A₁F⊥BE，
∴A₁F⊥面BCDE，
∵A₁F?面A'BE，
∴面A₁BE⊥面BCDE；
（2）解：连接CE，则
∵BE=CE=

2

，BC=2，
∴BE²+CE²=BC²，
∴CE⊥BE，
∵面A₁BE⊥面BCDE，面A₁BE∩面BCDE=BE，
∴CE⊥面A₁BE，
∴∠CA₁E为A₁C与面A₁BE所成角，
∴tan∠CA₁E=

CE

A1E

=

2

．

点评：本题考查线面垂直，考查面面垂直，考查线面角，考查学生分析解决问题的能力，考查学生的计算能力，正确运用面面垂直的判定定理是关键．