题目内容
己知
，
为平面上两个不共线的向量，p：|+|=|-|；q：⊥，则p是q的
- A.充要条件
- B.充分不必要条件
- C.必要不充分条件
- D.既不充分也不必要条件
A
分析：利用向量的三角形法则与平行四边形法则，说明p?q，利用⊥?p，得到结果．
解答：
解：因为，为平面上两个不共线的向量，p：|+|=|-|；
如图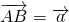
，
，
，
由向量的三角形法则与平行四边形法则可知，四边形是长方形，所以⊥，即p?q；
又⊥，所以|+|=|-|；即q?p；
所以p是q的充要条件．
故选A．
点评：本题考查充要条件的应用，向量的基本运算，是基础题．
分析：利用向量的三角形法则与平行四边形法则，说明p?q，利用
⊥?p，得到结果．解答：
解：因为，为平面上两个不共线的向量，p：|+|=|-|；如图
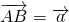，，，由向量的三角形法则与平行四边形法则可知，四边形是长方形，所以
⊥，即p?q；又
⊥，所以|+|=|-|；即q?p；所以p是q的充要条件．
故选A．
点评：本题考查充要条件的应用，向量的基本运算，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
己知
、
为平面上两个不共线的向量，p：|
+2
|=|
-2
|；q：
⊥
，则p是q的（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、既不充分也不必要条件 |
| D、充要条件 |
，
为平面上两个不共线的向量，p：|
+
|=|
-
|；q：
⊥
，则p是q的（ ）
、
为平面上两个不共线的向量，p：|
+2
|=|
-2
|；q：
⊥
，则p是q的（ ）
、
为平面上两个不共线的向量，p：|
+2
|=|
-2
|；q：
⊥
，则p是q的（ ）