题目内容
命题“若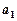 ,
,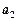
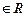 ,
,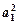
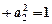 ,则
,则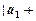
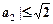 .”可以如下证明:构造函数
.”可以如下证明:构造函数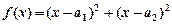 ,则
,则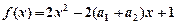 ,因为对一切
,因为对一切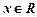 ,恒有
,恒有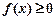 ,所以
,所以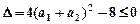 ,故得
,故得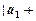
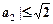 .
.
试解决下列问题:
(1)若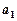 ,
,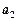 ,
,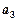
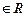 ,
,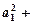
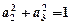 ,求证
,求证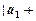
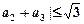 ;
;
(2)试将上述命题推广到n个实数,并证明你的结论.
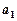 ,
,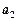
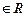 ,
,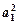
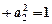 ,则
,则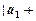
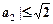 .”可以如下证明:构造函数
.”可以如下证明:构造函数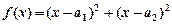 ,则
,则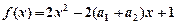 ,因为对一切
,因为对一切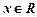 ,恒有
,恒有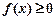 ,所以
,所以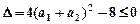 ,故得
,故得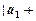
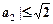 .
.试解决下列问题:
(1)若
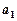 ,
,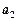 ,
,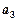
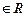 ,
,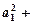
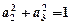 ,求证
,求证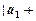
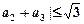 ;
;(2)试将上述命题推广到n个实数,并证明你的结论.
(1)同解析,(2)



(1)证明:构造函数
则

因为对一切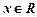 ,恒有
,恒有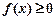 ,所以
,所以 ,
,
故得
 .
.
(2)推广:若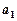 ,
,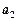 ,…,
,…,
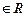 ,
,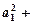
 ,
,
则
 .
.
证明:构造函数 ,
,
则
 .
.
因为对一切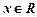 ,恒有
,恒有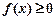 ,所以
,所以 ,
,
故得 .
.

则


因为对一切
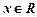 ,恒有
,恒有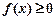 ,所以
,所以 ,
,故得

 .
. (2)推广:若
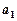 ,
,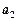 ,…,
,…,
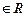 ,
,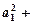
 ,
,则

 .
. 证明:构造函数
 ,
,则

 .
.因为对一切
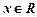 ,恒有
,恒有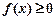 ,所以
,所以 ,
,故得
 .
. 
练习册系列答案
相关题目
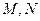 是椭圆
是椭圆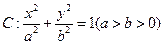 上关于原点
上关于原点 对称的两个点,点
对称的两个点,点 是椭圆
是椭圆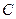 上任意一点,且直线
上任意一点,且直线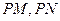 的斜率都存在(记为
的斜率都存在(记为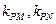 ),则
),则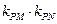 是与点
是与点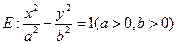 的类似性质,并加以证明。
的类似性质,并加以证明。 的实系数一元二次方程
的实系数一元二次方程 有两个虚根
有两个虚根 ,
, ,且
,且 (
( 为虚数单位),
为虚数单位), ,求实数
,求实数 的值.
的值. ,则第60个整数对是_______________.
,则第60个整数对是_______________. ,试通过计算
,试通过计算 来猜想
来猜想 的
的 _________________________.
_________________________. 中,
中, ,
, ,则
,则 ;
;
 A.
A.  B.
B.  C.
C.  D.
D. (
( 为虚数单位)所对应的点位于( )
为虚数单位)所对应的点位于( )