题目内容
等差数列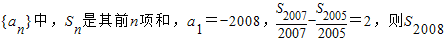 = .
= .
【答案】分析:由等差数列的性质S2n-1=(2n-1)an,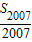 =a1004,
=a1004,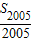 =a1003,则我们可以求出等差数列的公差,进而给出前n项和公式,代入即可求出S2008的值.
=a1003,则我们可以求出等差数列的公差,进而给出前n项和公式,代入即可求出S2008的值.
解答:解:∵在等差数列中S2n-1=(2n-1)an,
∴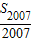 =a1004,
=a1004,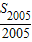 =a1003,
=a1003,
又∵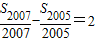
∴d=2,又由a1=-2008
∴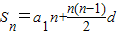 =n2-n-2008n,
=n2-n-2008n,
∴S2008=-2008
故答案为:-2008
点评:解答特殊数列(等差数列与等比数列)的问题时,根据已知条件构造关于基本量的方程,解方程求出基本量,再根据定义确定数列的通项公式及前n项和公式,然后代入进行运算.故熟练掌握等差数列的性质S2n-1=(2n-1)an,求出公差d,是快速解题的关键.
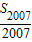 =a1004,
=a1004,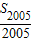 =a1003,则我们可以求出等差数列的公差,进而给出前n项和公式,代入即可求出S2008的值.
=a1003,则我们可以求出等差数列的公差,进而给出前n项和公式,代入即可求出S2008的值.解答:解:∵在等差数列中S2n-1=(2n-1)an,
∴
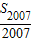 =a1004,
=a1004,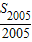 =a1003,
=a1003,又∵
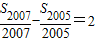
∴d=2,又由a1=-2008
∴
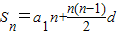 =n2-n-2008n,
=n2-n-2008n,∴S2008=-2008
故答案为:-2008
点评:解答特殊数列(等差数列与等比数列)的问题时,根据已知条件构造关于基本量的方程,解方程求出基本量,再根据定义确定数列的通项公式及前n项和公式,然后代入进行运算.故熟练掌握等差数列的性质S2n-1=(2n-1)an,求出公差d,是快速解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
数列{an}中,a2=2,a6=0且数列{
}是等差数列,则a4=( )
| 1 |
| an+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在等差数列{an}中,首项a1=0公差d≠0,若ak=S6,则k的值为( )
| A、15 | B、16 | C、17 | D、18 |