题目内容
12.在△ABC中,角A,B,C所对的边分别为a,b,c,若ac=$\frac{1}{4}$b2,sin A+sin C=psin B,且B为锐角,则实数p的取值范围是( )| A. | (1,$\sqrt{2}$) | B. | ($\frac{\sqrt{6}}{2}$,$\sqrt{2}$) | C. | ($\frac{\sqrt{6}}{2}$,$\sqrt{3}$) | D. | (1,$\sqrt{3}$) |
分析 根据正弦定理得a+c=pb,再利用余弦定理即可得出p2关于B的表达式,根据B的范围得出p的范围即可.
解答 解:∵sin A+sin C=psin B,∴a+c=pb,
由余弦定理,b2=a2+c2-2accos B=(a+c)2-2ac-2accos B=p2b2-$\frac{1}{2}$b2-$\frac{1}{2}$b2cos B,
即p2=$\frac{3}{2}$+$\frac{1}{2}$cos B,
∵0<cos B<1,∴p2∈($\frac{3}{2}$,2),
由题意知p>0,
∴p∈($\frac{\sqrt{6}}{2}$,$\sqrt{2}$),
选B.
点评 本题考查了正弦定理、余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
相关题目
20.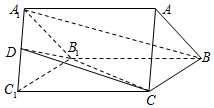 如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
(Ⅰ)求证:A1B∥平面B1CD;
(Ⅱ)当三棱锥C-B1C1D体积最大时,求点B到平面B1CD的距离.
 如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.(Ⅰ)求证:A1B∥平面B1CD;
(Ⅱ)当三棱锥C-B1C1D体积最大时,求点B到平面B1CD的距离.
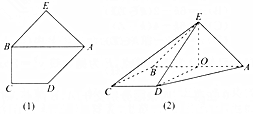 如图(1),在五边形BCDAE中,CD∥AB,∠BCD=90°,CD=BC=1,AB=2,△ABE是以AB为斜边的等腰直角三角形,现将△ABE沿AB折起,使平面ABE⊥平面ABCD,如图(2),记线段AB的中点为O.
如图(1),在五边形BCDAE中,CD∥AB,∠BCD=90°,CD=BC=1,AB=2,△ABE是以AB为斜边的等腰直角三角形,现将△ABE沿AB折起,使平面ABE⊥平面ABCD,如图(2),记线段AB的中点为O.