题目内容
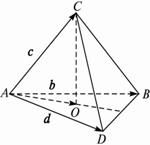
四面体ABCD中,∠DAC=∠BAC=∠BAD=60°,AC=AD=2,AB=3.(1)求直线AC和BD所成角的余弦值;
(2)求点C到平面ABD的距离.
解析:(1)![]() =d,
=d,![]() =b,
=b,![]() =c,?
=c,?
 ?
?
|c|=|d|=2,|b|=3,∴DB=b-d,?
∴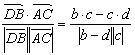
=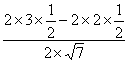 ?
?
=![]() .?
.?
∴DB与AC夹角的余弦值为![]() .?
.?
(2)设C在面ABD上的射影为O,?
设![]() =mb+nd,?
=mb+nd,?
∴![]() =mb+nd-c.?
=mb+nd-c.?
∵![]() =0,
=0,![]() =0,?
=0,?
∴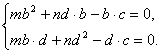 ?
?
∴![]() ?
?
∴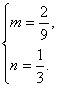
∴![]() =
=![]() b+
b+![]() d-c.?
d-c.?
∴![]()
=![]() .?
.?
∴C到平面ABD的距离为![]() .
.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
在四面体ABCD中,设AB=1,CD=2且AB⊥CD,若异面直线AB与CD间的距离为2,则四面体ABCD的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在四面体ABCD中,AB⊥平面ACD,BC=BD=5,AC=4,CD=
如图,在四面体ABCD中,AB⊥平面ACD,BC=BD=5,AC=4,CD= 如图,四面体ABCD中,O、E分别是BD、BC的中点,
如图,四面体ABCD中,O、E分别是BD、BC的中点,