Question

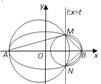已知如图椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

3

2

，椭圆的左、右两个顶点分别为A，B，AB=4，直线x=t（-2＜t＜2）与椭圆相交于M，N两点，经过三点A，M，N的圆与经过三点B，M，N的圆分别记为圆C1与圆C2．
（1）求椭圆的方程；
（2）求证：无论t如何变化，圆C1与圆C2的圆心距是定值；
（3）当t变化时，求圆C1与圆C2的面积的和S的最小值．

Answer 1

分析：（1）根据AB=4求得a，通过离心率求得c，进而可得b，求出椭圆的标准方程．
（2）根据题意可得A，B，M，N，P的坐标，进而可求得直线AM和PC₁的斜率，进而可求得直线PC₁的方程通过C₁和C₂的求得线段C₁C₂的长度为定值．
（3）根据两圆的半径求出关于t的圆C1与圆C2的面积的和S的关系式，根据t的范围可求得S的最小值．

解答：解：（1）由题意：

c

a

=

3

2

，2a=4可得：a=2，c=

3

，b2=a2-c2=1，
故所求椭圆方程为：

x2

4

+y2=1，
（2）易得A的坐标（-2，0），B的坐标（2，0），M的坐标(t，

4-t2

2

)，N的坐标(t，-

4-t2

2

)，
线段AM的中点P(

t-2

2

，

4-t2

4

)，
直线AM的斜率k₁=

4-t2 2

t+2

=

1

2

2-t 2+t

，
又PC₁⊥AM，∴直线PC₁的斜率k₂=-2

2+t 2-t

∴直线PC₁的方程y=-2

2+t 2-t

（x-

t-2

2

）+

4-t2

4

，
∴C₁的坐标为（

3t-6

8

，0）同理C₂的坐标为（

3t+6

8

，0），
∴|C₁C₂|=

3

2

，即无论t如何变化，为圆C1与圆C2的圆心距是定值．
（3）圆C₁的半径为|AC₁|=

3t+10

8

，圆C₂的半径为|BC₂|=

10-3t

8

，
则S=π|AC₁|²+π|BC₂|²=

π

32

（9t²+100）（-2＜t＜2）
显然t=0时，S最小，S_min=

25π

8

．

点评：本题主要考查了椭圆的标准方程．平时要多注意积累椭圆的几何性质，掌握用坐标法研究直线与椭圆，圆与椭圆的位置关系，熟练地求弦长、面积、对称等问题．