题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆的方程;
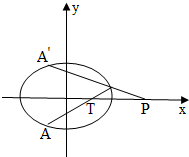
(2)如图,在椭圆C上任意取不同两点A,B,点A关于x轴的对称点为A′,若直线AB过定点T(2,0),求证:直线A′B过定点P(4,0).
分析:(1)由于椭圆C:
+
=1(a>b>0)过点(0,2),且离心率e=
.可得
,解得即可.
(2)设A(x1,y1),B(x2,y2).则A′(x1,-y1).由题意可知直线AB的斜率存在.
设直线AB的方程为:y=k(x-2),与联立与椭圆的方程联立可得根与系数的关系.
由直线A′B方程:y+y1=
(x-x1),令y=0,化为x=
,再利用y1=k(x1-2),y2=k(x2-2),
分别得到y1+y2=k(x1+x2-4),y1x2+y2x1=kx2(x1-2)+kx1(x2-2)=2k[x1x2-(x1+x2)].即可证明.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
|
(2)设A(x1,y1),B(x2,y2).则A′(x1,-y1).由题意可知直线AB的斜率存在.
设直线AB的方程为:y=k(x-2),与联立与椭圆的方程联立可得根与系数的关系.
由直线A′B方程:y+y1=
| y2+y1 |
| x2-x1 |
| y1x2+y2x1 |
| y1+y2 |
分别得到y1+y2=k(x1+x2-4),y1x2+y2x1=kx2(x1-2)+kx1(x2-2)=2k[x1x2-(x1+x2)].即可证明.
解答:解:(1)∵椭圆C:
+
=1(a>b>0)过点(0,2),且离心率e=
.
∴
,解得
.
∴椭圆C的标准方程为
+
=1.
(2)设A(x1,y1),B(x2,y2).则A′(x1,-y1).
由题意可知直线AB的斜率存在.
设直线AB的方程为:y=k(x-2),
联立
,化为(1+2k2)x2-8k2x+8k2-8=0,
∴x1+x2=
,x1x2=
.
由直线A′B方程:y+y1=
(x-x1),
令y=0,化为x=
,
∵y1=k(x1-2),y2=k(x2-2),
∴y1+y2=k(x1+x2-4)=
.
y1x2+y2x1=kx2(x1-2)+kx1(x2-2)=2k[x1x2-(x1+x2)]=2k•(
-
)=
.
∴x=
=4.即直线A′B过定点P(4,0).
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |

∴
|
|
∴椭圆C的标准方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)设A(x1,y1),B(x2,y2).则A′(x1,-y1).
由题意可知直线AB的斜率存在.
设直线AB的方程为:y=k(x-2),
联立
|
∴x1+x2=
| 8k2 |
| 1+2k2 |
| 8k2-8 |
| 1+2k2 |
由直线A′B方程:y+y1=
| y2+y1 |
| x2-x1 |
令y=0,化为x=
| y1x2+y2x1 |
| y1+y2 |
∵y1=k(x1-2),y2=k(x2-2),
∴y1+y2=k(x1+x2-4)=
| -4k |
| 1+2k2 |
y1x2+y2x1=kx2(x1-2)+kx1(x2-2)=2k[x1x2-(x1+x2)]=2k•(
| 8k2-8 |
| 1+2k2 |
| 8k2 |
| 1+2k2 |
| -16k |
| 1+2k2 |
∴x=
| ||
|
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、直线过定点问题等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目