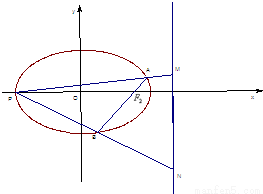
题目内容
如图,已知P是椭圆
+
=1(a>b>0)上且位于第一象限的一点,F是椭圆的右焦点,O是椭圆的中心,B是椭圆的上顶点,H是直线x=-
(c是椭圆的半焦距)与x轴的交点,若PF⊥OF,HB∥OP,试求椭圆的离心率的平方的值.
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
分析:依题意,可求得P(c,
),H(-
,0),利用HB∥OP求得c2=ab,再利用椭圆的性质即可求得e2.
| b2 |
| a |
| a2 |
| c |
解答:解:依题意,作图如下:
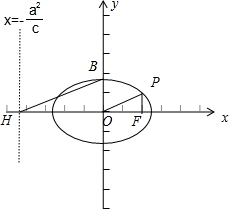
∵F(c,0)是椭圆的右焦点,PF⊥OF,
∴P(c,
),
∴直线OP的斜率k=
=
;
又H是直线x=-
(c是椭圆的半焦距)与x轴的交点,
∴H(-
,0),又B(0,b),
∴直线HB的斜率k′=
=
;
∵HB∥OP,
∴
=
,
∴c2=ab,又b2=a2-c2,
∴c4=a2b2=a2(a2-c2),
∴e4+e2-1=0,
∴e2=
.

∵F(c,0)是椭圆的右焦点,PF⊥OF,
∴P(c,
| b2 |
| a |
∴直线OP的斜率k=
| ||
| c-0 |
| b2 |
| ac |
又H是直线x=-
| a2 |
| c |
∴H(-
| a2 |
| c |
∴直线HB的斜率k′=
| b | ||
|
| bc |
| a2 |
∵HB∥OP,
∴
| b2 |
| ac |
| bc |
| a2 |
∴c2=ab,又b2=a2-c2,
∴c4=a2b2=a2(a2-c2),
∴e4+e2-1=0,
∴e2=
| ||
| 2 |
点评:本题考查椭圆的性质,利用HB∥OP求得c2=ab是关键,考查分析与计算能力,属于中档题.

练习册系列答案
相关题目
 (2011•江西模拟)如图,已知A是椭圆
(2011•江西模拟)如图,已知A是椭圆 上且位于第一象限的一点,F是椭圆的右焦点,O是椭圆的中心,B是椭圆的上顶点,H是直线
上且位于第一象限的一点,F是椭圆的右焦点,O是椭圆的中心,B是椭圆的上顶点,H是直线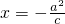 (c是椭圆的半焦距)与x轴的交点,若PF⊥OF,HB∥OP,试求椭圆的离心率的平方的值.
(c是椭圆的半焦距)与x轴的交点,若PF⊥OF,HB∥OP,试求椭圆的离心率的平方的值.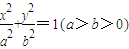 上的一个动点,F1,F2分别为椭圆的左、右焦点,弦AB过点F2,当AB⊥x轴时,恰好有|AF1|=3|AF2|.
上的一个动点,F1,F2分别为椭圆的左、右焦点,弦AB过点F2,当AB⊥x轴时,恰好有|AF1|=3|AF2|.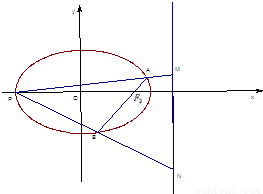
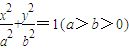 上的一个动点,F1,F2分别为椭圆的左、右焦点,弦AB过点F2,当AB⊥x轴时,恰好有|AF1|=3|AF2|.
上的一个动点,F1,F2分别为椭圆的左、右焦点,弦AB过点F2,当AB⊥x轴时,恰好有|AF1|=3|AF2|.