题目内容
如图,过抛物线y2=2px?(p＞0)的焦点F的直线l交抛物线于两点A、B,交其准线于C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
A.y2=
x B.y2=9x C.y2=
x D.y2=3x
答案:D
解析：过B作BD⊥抛物线的准线,垂足为D,则|BD|=|BF|.
∵|BC|=2|BF|=2|BD|,∴直线的倾斜角为60°,如图.
在Rt△AGF中,AG=3-p,AF=3,∠GAF=60°,
∴cos60°==.∴p=
.
∴抛物线方程为y2=3x.
练习册系列答案
相关题目
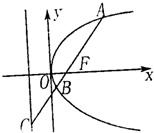如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为
78、如图，过抛物线y2=4x的焦点F的直线交抛物线与圆（x-1）2+y2=1于A，B，C，D四点，则|AB|•|CD|=
如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B（|AF|＞|BF|），交其准线于点C，若|BC|=2|BF|，且|AF|=2，则此抛物线的方程为
如图，过抛物线y2=2px（p＞0）的焦点F且倾斜角为60°的直线l交抛物线于A、B两点，若|AF|=3，则此抛物线方程为（ ）
如图，过抛物线y2=4x焦点的直线依次交抛物线与圆（x-1）2+y2=1于A，B，C，D，则