题目内容
5.已知数列{an}的各项均为正数,且a1=2,an=a${\;}_{n+1}^{2}$+4an+1+2(1)令bn=log2(an+2),证明:数列{bn}是等比数列
(2)设cn=nbn,求数列{cn}的前n项和Sn.
分析 (1)an=a${\;}_{n+1}^{2}$+4an+1+2,变形an+2=$({a}_{n+1}+2)^{2}$,又数列{an}的各项均为正数,两边取对数可得log2(an+2)=2log2(an+1+2),得到${b}_{n+1}=\frac{1}{2}{b}_{n}$,即可证明;
(2)由(1)可得:${b}_{n}=2×(\frac{1}{2})^{n-1}$=$\frac{1}{{2}^{n-2}}$,可得cn=nbn=$\frac{n}{{2}^{n-2}}$,利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 (1)证明:∵an=a${\;}_{n+1}^{2}$+4an+1+2,
∴an+2=$({a}_{n+1}+2)^{2}$,
又数列{an}的各项均为正数,
∴log2(an+2)=2log2(an+1+2),
∵bn=log2(an+2),bn+1=log2(an+1+2),
∴${b}_{n+1}=\frac{1}{2}{b}_{n}$,
∴数列{bn}是等比数列,首项为log2(2+2)=2,公比为$\frac{1}{2}$.
(2)解:由(1)可得:${b}_{n}=2×(\frac{1}{2})^{n-1}$=$\frac{1}{{2}^{n-2}}$,
∴cn=nbn=$\frac{n}{{2}^{n-2}}$,
∴数列{cn}的前n项和Sn=$2+2+\frac{3}{2}+\frac{4}{{2}^{2}}$+…+$\frac{n}{{2}^{n-2}}$,
$\frac{1}{2}{S}_{n}$=1+1+$\frac{3}{{2}^{2}}$+$\frac{4}{{2}^{3}}$+…+$\frac{n-1}{{2}^{n-2}}+\frac{n}{{2}^{n-1}}$,
∴$\frac{1}{2}{S}_{n}$=2+1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-2}}$-$\frac{n}{{2}^{n-1}}$=$\frac{2(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n-1}}$=$4-\frac{2+n}{{2}^{n-1}}$,
∴Sn=$8-\frac{2+n}{{2}^{n-2}}$.
点评 本题考查了“错位相减法”、等比数列的通项公式及其前n项和公式、对数的运算性质,考查了推理能力与计算能力,属于中档题.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |

| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
| A. | 已知两个命题p,q,若p∧q为假命题,则p∨q也为假命题 | |
| B. | 实数a=0是直线ax-2y=1与2ax-2y=3平行的充要条件 | |
| C. | “存在x∈R,使得x2+2x+5=0”的否定是“对任何x∈R,都有x2+2x+5≠0 | |
| D. | 命题p:?x∈R,x2+1≥1;命题q:?x∈R,x2-x+1≤0,则命题p∧(¬q)是真命题 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 的定义域为
的定义域为 ,以下命题正确的是( )
,以下命题正确的是( ) 与函数
与函数 的图象关于直线
的图象关于直线 对称;
对称; 的图象既关于点
的图象既关于点 成中心对称,对于任意
成中心对称,对于任意 ,又有
,又有 ,则
,则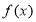 的图象关于直线
的图象关于直线 对称;
对称; ,满足关系式
,满足关系式 ,则函数
,则函数 是奇函数.
是奇函数.