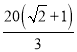题目内容
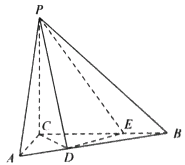
【题目】已知四棱锥![]() 中,底面ABCD是梯形,且
中,底面ABCD是梯形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,AD的中点为E,则四棱锥
,AD的中点为E,则四棱锥![]() 外接球的表面积为________.
外接球的表面积为________.
【答案】![]()
【解析】
由已知得,![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,那么DEBC是正方形,由
,那么DEBC是正方形,由![]() 平面
平面![]() ,可知
,可知![]() 平面
平面![]() ,可解得PB,可知
,可解得PB,可知![]() 是等边三角形,
是等边三角形,![]() 外接球的球心
外接球的球心![]() 到
到![]() 四点距离相等,设
四点距离相等,设![]() 在平面
在平面![]() 的投影为
的投影为![]() ,根据勾股定理可知点H是对角线的交点,在
,根据勾股定理可知点H是对角线的交点,在![]() 中可得
中可得![]() ,过
,过![]() 作
作![]() 于
于![]() ,再根据
,再根据![]() ,可求出
,可求出![]() ,由外接球面积公式即得。
,由外接球面积公式即得。
由题得,![]() ,
,![]() ,又
,又![]() ,
,![]() 四边形
四边形![]() 是正方形,
是正方形,![]() ,
,![]() 平面
平面![]() ,又
,又![]()
![]() ,
,![]()
![]() 平面
平面![]() ,所以
,所以![]() .则有
.则有![]() ,即
,即![]() ,解得
,解得![]() .
.![]() 球心
球心![]() 到
到![]() 四点距离相等,设
四点距离相等,设![]() 在平面
在平面![]() 的投影为
的投影为![]() ,那么
,那么![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() ,则有
,则有![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]()
![]() ,
,![]()
![]() .
.![]()
![]() 是正方形,
是正方形,![]() 平面
平面![]() 上且到
上且到![]() 四点距离相等的点即为正方形
四点距离相等的点即为正方形![]() 的对称中心,即对角线的交点,则
的对称中心,即对角线的交点,则![]() .
.![]()
![]() .过
.过![]() 作
作![]() 于
于![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() ,
,![]()
![]() 平面
平面![]() ,即
,即![]() 是点
是点![]() 在平面
在平面![]() 的投影.
的投影.![]()
![]() 是等边三角形,
是等边三角形,![]()
![]() ,
,![]() ,
,![]()
![]() ,与
,与![]() 联立解得
联立解得![]() ,则
,则![]() .
.
故答案为:![]()

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目