题目内容
【题目】已知函数![]() ,(其中
,(其中![]() )的图象关于点
)的图象关于点![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,则对于下列判断:
,则对于下列判断:
①直线![]() 是函数
是函数![]() 图象的一条对称轴;
图象的一条对称轴;
②点![]() 是函数
是函数![]() 的一个对称中心;
的一个对称中心;
③函数![]() 与
与![]() 的图象的所有交点的横坐标之和为
的图象的所有交点的横坐标之和为![]() .
.
其中所有正确的判断是( )
A.①②B.①③C.②③D.②
【答案】C
【解析】
先根据图象关于点![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,分别代入求解计算出
,分别代入求解计算出![]() 的解析式,再根据三角函数的图像性质逐个判断即可.
的解析式,再根据三角函数的图像性质逐个判断即可.
因为![]() 的图象关于点
的图象关于点![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,故
,故![]() 且
且![]() ,故
,故![]() .所以
.所以![]() .
.
故![]() .又图像最低点为
.又图像最低点为![]() ,故
,故![]() .
.
即![]() .又
.又![]() ,故
,故![]() .故
.故![]() .
.
对①,当![]() 时
时![]() ,不是正弦函数的对称轴.故①错误.
,不是正弦函数的对称轴.故①错误.
对②,当![]() 时,
时,![]() ,故点
,故点![]() 是函数
是函数![]() 的一个对称中心,故②正确.
的一个对称中心,故②正确.
对③,因为![]() ,故
,故![]() ,所以函数
,所以函数![]() 与
与![]() 有6个交点.设交的横坐标分别为
有6个交点.设交的横坐标分别为![]() ,根据图像以及五点作图法的方法可知,当
,根据图像以及五点作图法的方法可知,当![]() 时解得
时解得![]() 为6个横坐标
为6个横坐标![]() 的对称轴.
的对称轴.
故![]() .故③正确.
.故③正确.
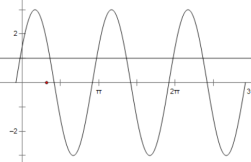
综上,②③正确.
故选:C

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目