题目内容
 如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若
如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若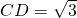 ,AB=AC=2,则线段AD的长是________;圆O的半径是________.
,AB=AC=2,则线段AD的长是________;圆O的半径是________.
1 2
分析:①由切割线定理得CD2=DA•DB,即可得出DA;②由余弦定理可得∠DCA,利用弦切角定理可得∠ABC=∠DCA,再利用正弦定理得 即可.
即可.
解答:①∵CD是⊙O的切线,由切割线定理得CD2=DA•DB,CD= ,DB=DA+AB=DA+2,
,DB=DA+AB=DA+2,
∴ ,又DA>0,解得DA=1.
,又DA>0,解得DA=1.
②在△ACD中,由余弦定理可得cos∠ACD= =
= =
= ,
,
∵0<∠ACD<π,∴ .
.
根据弦切角定理可得∠ABC=∠DCA= .
.
由正弦定理可得 =
= =4,∴R=2.
=4,∴R=2.
故答案分别为1,2.
点评:熟练掌握切割线定理、弦切角定理、正弦定理、余弦定理是解题的关键.
分析:①由切割线定理得CD2=DA•DB,即可得出DA;②由余弦定理可得∠DCA,利用弦切角定理可得∠ABC=∠DCA,再利用正弦定理得
 即可.
即可.解答:①∵CD是⊙O的切线,由切割线定理得CD2=DA•DB,CD=
 ,DB=DA+AB=DA+2,
,DB=DA+AB=DA+2,∴
 ,又DA>0,解得DA=1.
,又DA>0,解得DA=1.②在△ACD中,由余弦定理可得cos∠ACD=
 =
= =
= ,
,∵0<∠ACD<π,∴
 .
.根据弦切角定理可得∠ABC=∠DCA=
 .
.由正弦定理可得
 =
= =4,∴R=2.
=4,∴R=2.故答案分别为1,2.
点评:熟练掌握切割线定理、弦切角定理、正弦定理、余弦定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2
如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2 如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P. 如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2
如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2 (2012•通州区一模)如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,AB=BC=3,CD=2
(2012•通州区一模)如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,AB=BC=3,CD=2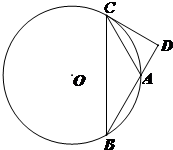 (2013•朝阳区一模)如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若
(2013•朝阳区一模)如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若