题目内容
（2012•通州区一模）如图，圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，AB=BC=3，CD=2| 10 |
| 7 |
| 25 |
| 10 |
| 7 |
| 25 |
| 10 |
分析：利用切割线定理，先求出DB的长，再利用余弦定理求cosD．
解答：解：如图，∵圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，
AB=BC=3，CD=2
，
∴CD2=DB•DA，
∴DB（DB+3）=40，
解得DB=5，或DB=-8（舍），
∴cosD=
=
=
．
故答案为：
．
如图，∵圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，AB=BC=3，CD=2
| 10 |
∴CD2=DB•DA，
∴DB（DB+3）=40，
解得DB=5，或DB=-8（舍），
∴cosD=
| CD2+DB2-BC2 |
| 2•CD•DB |
=
| 40+25-9 | ||
2×2
|
7
| ||
| 25 |
故答案为：
7
| ||
| 25 |
点评：本题考查与圆有关的比例线段的应用，解题时要认真审题，仔细解答，注意切割线定理和余弦定理的灵活运用．
练习册系列答案
相关题目
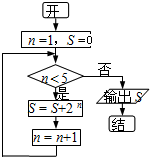（2012•通州区一模）如图，程序框图所进行的求和运算是（ ）