题目内容
已知f(x)=2sin(2x+ )+a+1(a为常数).
)+a+1(a为常数).
(1)求f(x)的递增区间;
(2)若x∈[0, ]时,f(x)的最大值为4,求a的值;
]时,f(x)的最大值为4,求a的值;
(3)求出使f(x)取最大值时x的集合.
解(1)当2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,
即kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈Z时,f(x)单调递增,
,k∈Z时,f(x)单调递增,

∴当sin(2x+ )=1时,f(x)有最大值为2×1+a+1=4,∴a=1;
)=1时,f(x)有最大值为2×1+a+1=4,∴a=1;
(3)当x∈R,f(x)取最大值时,2x+ =
= +2kπ,k∈Z,∴x=
+2kπ,k∈Z,∴x= +kπ,k∈Z,
+kπ,k∈Z,
∴当x∈R,使f(x)取得最大值时x的集合为{x|x= +kπ,k∈Z}.
+kπ,k∈Z}.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 ,
, 表示不小于
表示不小于 .定义在
.定义在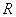 上的函数
上的函数 ,若集合
,若集合 ,则集合
,则集合 中所有元素的和为 .
中所有元素的和为 . 被圆
被圆 截得的弦长为__________
截得的弦长为__________ 是 ( )
是 ( ) 的奇函数 B.周期为
的奇函数 B.周期为 的奇函数 D.周期为
的奇函数 D.周期为 的偶函数
的偶函数 ,则
,则 __________.
__________. ,
, ,则
,则 .
.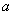 ,b,c.若
,b,c.若 ,
, ,则角
,则角 =
=
 中,已知
中,已知 .
. ;
;  求角A的大小.
求角A的大小.