题目内容
已知椭圆┍的方程为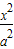 +
+ =1(a>b>0),点P的坐标为(-a,b).
=1(a>b>0),点P的坐标为(-a,b).(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足
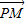 =
= (
( +
+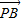 ),求点M的坐标;
),求点M的坐标;(2)设直线l1:y=k1x+p交椭圆┍于C、D两点,交直线l2:y=k2x于点E.若k1•k2=-
 ,证明:E为CD的中点;
,证明:E为CD的中点;(3)对于椭圆┍上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆┍上存在不同的两个交点P1、P2满足
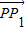 +
+ =
=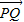 ,写出求作点P1、P2的步骤,并求出使P1、P2存在的θ的取值范围.
,写出求作点P1、P2的步骤,并求出使P1、P2存在的θ的取值范围.
【答案】分析:(1)设M(x,y) 根据 =
= (
(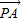 +
+ )分别用三点的坐标表示出三个向量,进而解得x和y,则M点坐标可得.
)分别用三点的坐标表示出三个向量,进而解得x和y,则M点坐标可得.
(2)直线l1与椭圆方程联立消去y,根据判别式求得,a2k12+b2-p2>0,设C(x1,y1)、D(x2,y2),CD中点坐标为(x,y),利用韦达定理可求得x1+x2的表达式,进而求得x,代入直线方程求得y,两直线方程联立根据直线l2的斜率求得x=x,y=y
进而判断出E为CD的中点;
(3)先求出PQ的中点的坐标,进而求出直线OE的斜率,再由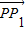 +
+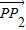 =
=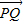 ,知E为CD的中点,根据(2)可得CD的斜率,直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标.欲使P1、P2存在,必须点E在椭圆内,进而求得q的取值范围.
,知E为CD的中点,根据(2)可得CD的斜率,直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标.欲使P1、P2存在,必须点E在椭圆内,进而求得q的取值范围.
解答:解:(1)设M(x,y)
∵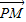 =
= (
(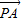 +
+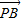 ),
),
∴2(x+a,y-b)=(a,-2b)+(2a,-b)
∴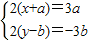 ,
,
解得x=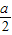 y=-
y=-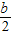
M点坐标为(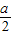 ,-
,-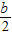 )
)
(2)由方程组 ,消y得方程(a2k′1+b2)x2+2a2k1px+a2(p2-b2)=0,
,消y得方程(a2k′1+b2)x2+2a2k1px+a2(p2-b2)=0,
因为直线l1:y=k1x+p交椭圆于C、D两点,所以△>0,即a2k12+b2-p2>0,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x,y),
则x=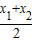 =-
=-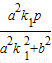 ,y=k1x+p=
,y=k1x+p=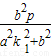 ,由方程组
,由方程组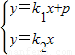 ,消y得方程(k2-k1)x=p,
,消y得方程(k2-k1)x=p,
又因为k2=- ,所以x=
,所以x=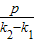 =x,y=k2x=y
=x,y=k2x=y
故E为CD的中点;
(3)求作点P1、P2的步骤:
1°求出PQ的中点E(-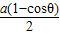 ,
,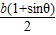 ),
),
2°求出直线OE的斜率k2=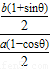 =
=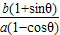 ,
,
3°由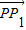 +
+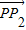 =
=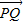 ,知E为CD的中点,根据(2)可得CD的斜率k1=
,知E为CD的中点,根据(2)可得CD的斜率k1=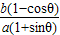 ,
,
4°从而得直线P1P2的方程:y-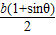 =
=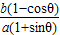 (x+
(x+ ),
),
5°将直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标.
欲使P1、P2存在,必须点E在椭圆内,
所以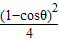 +
+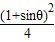 <1,化简得sinθ-cosθ<
<1,化简得sinθ-cosθ< ,∴sin(θ-
,∴sin(θ-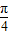 )<
)<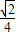 ,
,
又0<q<p,所以-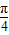 <θ-
<θ-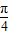 <arcsin
<arcsin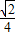 ,
,
故q的取值范围是(0,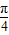 +arcsin
+arcsin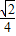 )
)
点评:本题主要考查了直线与圆锥曲线的综合问题.解题的前提是要求学生对基础知识有相当熟练的把握.
 =
= (
(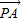 +
+ )分别用三点的坐标表示出三个向量,进而解得x和y,则M点坐标可得.
)分别用三点的坐标表示出三个向量,进而解得x和y,则M点坐标可得.(2)直线l1与椭圆方程联立消去y,根据判别式求得,a2k12+b2-p2>0,设C(x1,y1)、D(x2,y2),CD中点坐标为(x,y),利用韦达定理可求得x1+x2的表达式,进而求得x,代入直线方程求得y,两直线方程联立根据直线l2的斜率求得x=x,y=y
进而判断出E为CD的中点;
(3)先求出PQ的中点的坐标,进而求出直线OE的斜率,再由
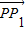 +
+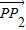 =
=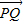 ,知E为CD的中点,根据(2)可得CD的斜率,直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标.欲使P1、P2存在,必须点E在椭圆内,进而求得q的取值范围.
,知E为CD的中点,根据(2)可得CD的斜率,直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标.欲使P1、P2存在,必须点E在椭圆内,进而求得q的取值范围.解答:解:(1)设M(x,y)
∵
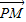 =
= (
(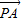 +
+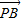 ),
),∴2(x+a,y-b)=(a,-2b)+(2a,-b)
∴
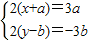 ,
,解得x=
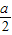 y=-
y=-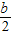
M点坐标为(
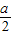 ,-
,-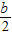 )
)(2)由方程组
 ,消y得方程(a2k′1+b2)x2+2a2k1px+a2(p2-b2)=0,
,消y得方程(a2k′1+b2)x2+2a2k1px+a2(p2-b2)=0,因为直线l1:y=k1x+p交椭圆于C、D两点,所以△>0,即a2k12+b2-p2>0,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x,y),
则x=
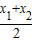 =-
=-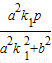 ,y=k1x+p=
,y=k1x+p=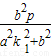 ,由方程组
,由方程组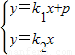 ,消y得方程(k2-k1)x=p,
,消y得方程(k2-k1)x=p,又因为k2=-
 ,所以x=
,所以x=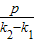 =x,y=k2x=y
=x,y=k2x=y故E为CD的中点;
(3)求作点P1、P2的步骤:
1°求出PQ的中点E(-
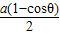 ,
,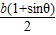 ),
),2°求出直线OE的斜率k2=
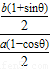 =
=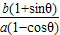 ,
,3°由
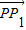 +
+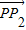 =
=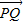 ,知E为CD的中点,根据(2)可得CD的斜率k1=
,知E为CD的中点,根据(2)可得CD的斜率k1=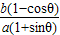 ,
,4°从而得直线P1P2的方程:y-
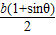 =
=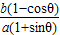 (x+
(x+ ),
),5°将直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标.
欲使P1、P2存在,必须点E在椭圆内,
所以
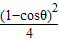 +
+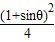 <1,化简得sinθ-cosθ<
<1,化简得sinθ-cosθ< ,∴sin(θ-
,∴sin(θ-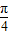 )<
)<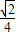 ,
,又0<q<p,所以-
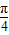 <θ-
<θ-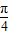 <arcsin
<arcsin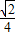 ,
,故q的取值范围是(0,
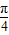 +arcsin
+arcsin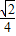 )
)点评:本题主要考查了直线与圆锥曲线的综合问题.解题的前提是要求学生对基础知识有相当熟练的把握.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
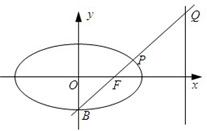 如图,已知椭圆C的方程为:
如图,已知椭圆C的方程为: 已知椭圆C的方程为
已知椭圆C的方程为