题目内容
14.计算$\frac{3x}{{x}^{2}-2x-3}$-$\frac{1}{x+1}$=3.分析 按照分式方程的解法与步骤,解方程即可.
解答 解:∵$\frac{3x}{{x}^{2}-2x-3}$-$\frac{1}{x+1}$=3,
∴$\frac{3x-(x-3)}{(x+1)(x-3)}$=3,
∴3x-(x-3)=3(x+1)(x-3),
化简得3x2-8x-12=0,
解得x=$\frac{4+2\sqrt{13}}{3}$或x=$\frac{4-2\sqrt{13}}{3}$;
经检验x=$\frac{4+2\sqrt{13}}{3}$和x=$\frac{4-2\sqrt{13}}{3}$都是原方程的解.
点评 本题考查了分式方程的解法与应用问题,解题时应注意检验是否为方程的根,是基础题目.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
4.有以下程序:若输入的值为3,5,则执行此程序后输出的值为( )


| A. | 3,5 | B. | 5,3 | C. | 3,3 | D. | 5,5 |
10. 如图,网格纸上小正方形的边长为,粗实线和虚线画出的是某四面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )
如图,网格纸上小正方形的边长为,粗实线和虚线画出的是某四面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )
 如图,网格纸上小正方形的边长为,粗实线和虚线画出的是某四面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )
如图,网格纸上小正方形的边长为,粗实线和虚线画出的是某四面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{2}$ | C. | 6 | D. | 4$\sqrt{3}$ |
7.已知函数f(x)=x2-ax的图象在点A(1,f(1))处的切线l与直线x+3y-1=0垂直,记数列$\{\frac{1}{f(n)}\}$的前n项和为Sn,则S2016的值为( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2014}{2015}$ | D. | $\frac{2017}{2018}$ |
8.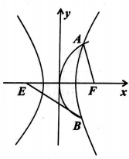 已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
 已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )| A. | 4-$\sqrt{7}$ | B. | 4-$\sqrt{3}$ | C. | 4+$\sqrt{3}$ | D. | 4+$\sqrt{7}$ |