题目内容
11.已知点F(c,0)(c>0)是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点,F关于直线y=$\sqrt{3}$x的对称点A也在该椭圆上,则该椭圆的离心率是( )| A. | $\sqrt{3}$+2 | B. | $\sqrt{3}$-1 | C. | -$\sqrt{3}$+1 | D. | -$\sqrt{3}$+2 |
分析 求出F(c,0)关于直线y=$\sqrt{3}$x的对称点A的坐标,代入椭圆方程可得离心率.
解答 解:设F(c,0)关于直线y=$\sqrt{3}$x的对称点A(x1,y1),
则$\frac{{y}_{1}}{2}$=$\frac{\sqrt{3}}{2}$(x1+c)①,且$\frac{{y}_{1}}{{x}_{1}-c}$=-$\frac{\sqrt{3}}{3}$②.
联立①②解得:x1=-$\frac{1}{2}$c,y1=$\frac{\sqrt{3}}{2}$c,即A(-$\frac{c}{2}$,$\frac{\sqrt{3}}{2}$c),
代入椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1得:$\frac{\frac{{c}^{2}}{4}}{{a}^{2}}$+$\frac{\frac{3{c}^{2}}{4}}{{b}^{2}}$=1.
由e=$\frac{c}{a}$,b2=a2-c2,
化简可得e4-8e2+4=0,
解得:e=$\sqrt{3}$-1.
故选:B.
点评 本题考查椭圆的方程和简单性质的应用,考查对称知识以及计算能力,是中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 已知角β的终边在图中阴影所表示的范围内(不包括边界),那么β∈(K•180°+30°,K•180°+150°),k∈Z..
已知角β的终边在图中阴影所表示的范围内(不包括边界),那么β∈(K•180°+30°,K•180°+150°),k∈Z..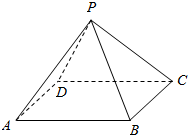 如图,P-ABCD是一个各棱长都为2cm的正四棱锥,求这个棱锥的表面积和体积.
如图,P-ABCD是一个各棱长都为2cm的正四棱锥,求这个棱锥的表面积和体积.