题目内容
10．若f（cosx）=-1-2cos3x，求f（sinx）．分析 由已知条件利用三角函数的诱导公式和函数的性质求解．
解答 解：∵f（cosx）=-1-2cos3x，
∴f（sinx）=f（cos（$\frac{π}{2}$-x））
=1-2cos（$\frac{3π}{2}-3x$）
=1+2sin3x．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意三角函数的诱导公式和函数的性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
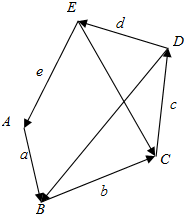向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$，$\overrightarrow{d}$，$\overrightarrow{e}$如图所示，解答下列各题：
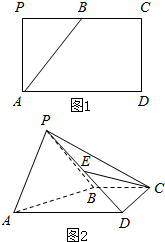如图1，矩形APCD中，AD=2AP，B为PC的中点，将△APB折沿AB折起，使得PD=PC，如图2．
11．已知点F（c，0）（c＞0）是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点，F关于直线y=$\sqrt{3}$x的对称点A也在该椭圆上，则该椭圆的离心率是（ ）
| A． | $\sqrt{3}$+2 | B． | $\sqrt{3}$-1 | C． | -$\sqrt{3}$+1 | D． | -$\sqrt{3}$+2 |