题目内容
 如图,在?ABCD中,E是AB延长线上一点,DE交AC于G,交BC于F.
如图,在?ABCD中,E是AB延长线上一点,DE交AC于G,交BC于F.
求证:(1)DG2=GE•GF;
(2) =
= .
.
证明:(1)∵CD∥AE,
∴ =
=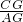 .
.
又∵AD∥CF,
∴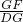 =
=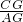 .
.
∴ =
=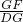 ,
,
即DG2=GE•GF.
(2)∵BF∥AD,
∴ =
=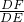 .①
.①
又∵CD∥BE,∴ =
=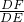 .②
.②
由①②可得 =
= .
.
分析:(1)根据平行四边形两条对边平行,得到两对相似三角形.写出对应边成比例,得到两个比例式中各有两条线段的比相等,根据等量代换得到比例式,转化成乘积式,得到结论.
(2)做法同一类似,根据两条线段平行,根据平行得到对应线段成比例,在两个比例式中出现有一个比例相等,利用等量代换,得到结论.
点评:本题考查平行线分线段成比例定理,在题目中连续使用成比例定理,有两次使用等量代换,是一个比较典型的题目,实际上证明线段成比例是学习中的难点.
∴
 =
=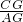 .
.又∵AD∥CF,
∴
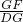 =
=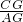 .
.∴
 =
=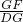 ,
,即DG2=GE•GF.
(2)∵BF∥AD,
∴
 =
=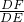 .①
.①又∵CD∥BE,∴
 =
=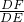 .②
.②由①②可得
 =
= .
.分析:(1)根据平行四边形两条对边平行,得到两对相似三角形.写出对应边成比例,得到两个比例式中各有两条线段的比相等,根据等量代换得到比例式,转化成乘积式,得到结论.
(2)做法同一类似,根据两条线段平行,根据平行得到对应线段成比例,在两个比例式中出现有一个比例相等,利用等量代换,得到结论.
点评:本题考查平行线分线段成比例定理,在题目中连续使用成比例定理,有两次使用等量代换,是一个比较典型的题目,实际上证明线段成比例是学习中的难点.

练习册系列答案
相关题目
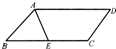 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )| A、3和2 | B、2和3 | C、4和1 | D、1和4 |
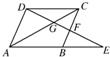 如图,在?ABCD中,E是AB延长线上一点,DE交AC于G,交BC于F.
如图,在?ABCD中,E是AB延长线上一点,DE交AC于G,交BC于F.
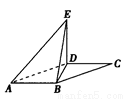
 ,用a,b表示
,用a,b表示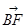 和
和 。
。