Question

(本小题满分12分)

如图，在□ABCD中，∠DAB=60°，AB=2，AD="4." 将△CBD沿BD折起到△EBD的位置，使平面EBD⊥平面ABD.

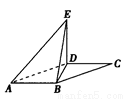
(1)求证：AB⊥DE；

(2)求三棱锥E—ABD的侧面积.

 

Answer 1

【答案】

（1）先求出BD，利用勾股定理知AB⊥BD，再由面面垂直的性质知AB⊥平面EBD，从而得证（2）S=8+2

【解析】

试题分析：(1)在△ABD 中，∵AB=2，AD=4，∠DAB=60°，

∴BD=.

∴AB²+BD²=AD²，∴AB⊥BD.

又∵平面EBD⊥平面ABD，

平面EBD∩平面ABD=BD，AB平面ABD，

∴AB⊥平面EBD. 又∵DE平面EBC，∴AB⊥DE.                                ……5分

(2)由(1)知AB⊥BD.

∵CD∥AB    ∴CD⊥BD，从而DE⊥BD

在Rt△DBE中, ∵DB=2，DE=DC=AB=2，

∴S_△DBE=.……7分

又∵AB⊥平面EBD，BE平面EBD，∴AB⊥BE.

∵BE=BC=AD=4，S_△ABE=AB·BE=4……9分

∵DE⊥BD，平面EBD⊥平面ABD，∴ED⊥平面ABD，

而AD平面ABD，∴ED⊥AD，∴S_△ADE=AD·DE="4."                            ……11分

综上，三棱锥E—ABD的侧面积S=8+2.                                  ……12分

考点：本小题主要考查空间中直线、平面间的位置关系的判断和证明以及侧面积的计算，考查学生的空间想象能力和推理论证能力以及运算求解能力.

点评：要证明空间中直线、平面间的位置关系要紧扣判定定理和性质定理，定理中要求的条件缺一不可.