题目内容
【题目】已知函数f（x）=|x|﹣|2x﹣1|，记f（x）＞﹣1的解集为M．
（1）求M；
（2）已知a∈M，比较a2﹣a+1与 
的大小．
【答案】
（1）解：f（x）=|x|﹣|2x﹣1|=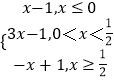 
，由f（x）＞﹣1，可得： 
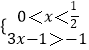或 
或 
，
解得0＜x＜2，∴M=（0，2）．
（2）解：由（1）知：0＜a＜2，∵a2﹣a+1﹣ 
= 
=g（a）．
当0＜a＜1时，g（a）＜0，∴a2﹣a+1＜ ；
当a=1时，g（a）=0，∴a2﹣a+1= ；
当1＜a＜2时，g（a）＞0，∴a2﹣a+1＞ ；
综上所述：当0＜a＜1时，∴a2﹣a+1＜ ；
当a=1时，a2﹣a+1= ；
当1＜a＜2时，a2﹣a+1＞
【解析】（1）f（x）=|x|﹣|2x﹣1|= 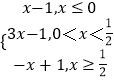，由f（x，由f（x）＞﹣1，可得： 
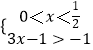或 
或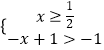 
，解出即可得出．（2）由（1）知：0＜a＜2，可得：a2﹣a+1﹣ = =g（a）．对a分类讨论：当0＜a＜1时，当a=1时，当1＜a＜2时，即可得出．
练习册系列答案
相关题目
