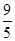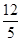题目内容
设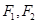 是双曲线
是双曲线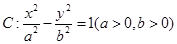 的两个焦点,
的两个焦点, 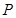 是
是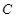 上一点,若
上一点,若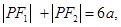 且
且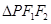 的最小内角为
的最小内角为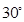 ,则
,则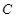 的离心率为( )
的离心率为( )
A.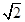 | B.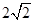 | C.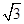 | D.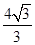 |
C
解析试题分析:由题意得 ,由条件得
,由条件得 ,由正弦定理得,
,由正弦定理得, ,∴
,∴ ,∴
,∴ ,在
,在 中,
中, ,∴
,∴ ,故选C.
,故选C.
考点:1.双曲线的标准方程和几何性质;2.正弦定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若椭圆 上有
上有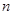 个不同的点
个不同的点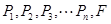 为右焦点,
为右焦点, 组成公差
组成公差 的等差数列,则
的等差数列,则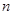 的最大值为( )
的最大值为( )
| A.199 | B.200 | C.99 | D.100 |
直线y=x与椭圆C: +
+ =1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )
=1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )
A. | B. |
C. | D. |
设M(x0,y0)为抛物线C:y2=8x上一点,F为抛物线C的焦点,若以F为圆心,|FM|为半径的圆和抛物线C的准线相交,则x0的取值范围是( )
| A.(2,+∞) | B.(4,+∞) |
| C.(0,2) | D.(0,4) |
如果双曲线的两个焦点分别为F1(-3,0),F2(3,0),一条渐近线方程为y=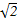 x,那么它的两条准线间的距离是( )
x,那么它的两条准线间的距离是( )
A.6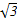 | B.4 | C.2 | D.1 |
直线y=x-3与抛物线y2=4x交于A,B两点,过A,B两点向抛物线的准线作垂线,垂足分别为P,Q,则梯形APQB的面积为( )
| A.48 | B.56 | C.64 | D.72 |
 (B)
(B)  (C)
(C)  (D)
(D) 
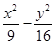 =1上的点,点M满足|
=1上的点,点M满足| 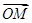 |=1,且
|=1,且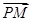 =0,则当|
=0,则当|