题目内容
已知:正数数列an中,若关于x的方程 有相等的实根
有相等的实根(1)若a1=1,求a2,a3的值;并证明

(2)若a1=a,bn=an-(3n-12)•2n,求使bn+1≥bn对一切n∈N+都成立的a的取值范围.
【答案】分析:(1)由 得an+1=3an+2,再由an+1=3an+2得an+1+1=3(a1+1),由此能够证明
得an+1=3an+2,再由an+1=3an+2得an+1+1=3(a1+1),由此能够证明 .
.
(2)当a1=a时,an+1=(a+1)•3n-1,bn=(a+1)•3n-1-1-(3n-12)•2n,bn+1-bn=(a+1)•2•3n-1-(3n-6)•2n≥0对一切n∈N+都成立,由此能求出使bn+1≥bn对一切n∈N+都成立的a的取值范围.
解答:解:(1)由 得an+1=3an+2∴
得an+1=3an+2∴
由an+1=3an+2得an+1+1=3(a1+1),
所以an+1为首项为2公比为3的等比数列
得an+1=2•3n-1(5分),
 (8分)
(8分)
(2)当a1=a时,an+1=(a+1)•3n-1,bn=(a+1)•3n-1-1-(3n-12)•2n
bn+1-bn=(a+1)•2•3n-1-(3n-6)•2n≥0对一切n∈N+都成立,所以
令 ,
, ,
,
所以 ,所以
,所以 (16分)
(16分)
点评:本题考查数列的性质和综合运用,解题时要注意公式的合理运用.
 得an+1=3an+2,再由an+1=3an+2得an+1+1=3(a1+1),由此能够证明
得an+1=3an+2,再由an+1=3an+2得an+1+1=3(a1+1),由此能够证明 .
.(2)当a1=a时,an+1=(a+1)•3n-1,bn=(a+1)•3n-1-1-(3n-12)•2n,bn+1-bn=(a+1)•2•3n-1-(3n-6)•2n≥0对一切n∈N+都成立,由此能求出使bn+1≥bn对一切n∈N+都成立的a的取值范围.
解答:解:(1)由
 得an+1=3an+2∴
得an+1=3an+2∴
由an+1=3an+2得an+1+1=3(a1+1),
所以an+1为首项为2公比为3的等比数列
得an+1=2•3n-1(5分),
 (8分)
(8分)(2)当a1=a时,an+1=(a+1)•3n-1,bn=(a+1)•3n-1-1-(3n-12)•2n
bn+1-bn=(a+1)•2•3n-1-(3n-6)•2n≥0对一切n∈N+都成立,所以

令
 ,
, ,
,所以
 ,所以
,所以 (16分)
(16分)点评:本题考查数列的性质和综合运用,解题时要注意公式的合理运用.

练习册系列答案
相关题目
 在抛物线y2=x+1上;数列{bn}中,点Bn(n,bn)在过点(0,1),以方向向量为(1,2)的直线上.
在抛物线y2=x+1上;数列{bn}中,点Bn(n,bn)在过点(0,1),以方向向量为(1,2)的直线上. ,问是否存在k∈N,使f(k+27)=4f(k)成立,若存在,求出k值;若不存在,说明理由;(文理共答)
,问是否存在k∈N,使f(k+27)=4f(k)成立,若存在,求出k值;若不存在,说明理由;(文理共答)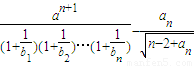 ≤0成立,求正数a的取值范围.(只理科答)
≤0成立,求正数a的取值范围.(只理科答)