题目内容
已知f(x)=ex-t(x+1).
(1)若f(x)≥0对一切正实数x恒成立,求t的取值范围;
(2)设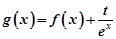 ,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
(3)求证: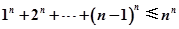 (n∈N*).
(n∈N*).
(1)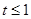 ;(2)
;(2)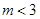 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)对函数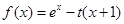 求导数,分离变量得
求导数,分离变量得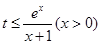 ,再设
,再设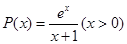 ,用导数法判断
,用导数法判断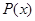 的单调性、极值,从而求出
的单调性、极值,从而求出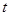 的取值范围;(2)设x1、x2是任意的两实数,且x1<x2,
的取值范围;(2)设x1、x2是任意的两实数,且x1<x2,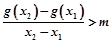 ,则
,则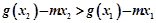 ,构造函数
,构造函数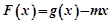 ,则函数
,则函数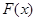 在
在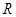 上是增函数,即
上是增函数,即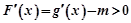 恒成立,即对任意的t≤-1,x∈R,
恒成立,即对任意的t≤-1,x∈R,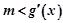 恒成立,再用均值不等式求
恒成立,再用均值不等式求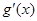 的最小值,从而求得
的最小值,从而求得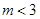 ;(3)由(1)知,
;(3)由(1)知,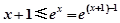 ,得
,得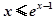 ,令
,令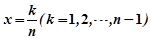 ,放缩得
,放缩得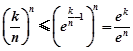 ,把
,把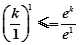
取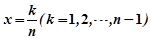 ,则
,则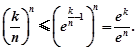
取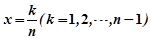 ,则
,则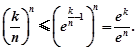
而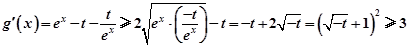 用导数法
用导数法
(1) (x>0)恒成立.
(x>0)恒成立.
设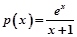 (x≥0),则
(x≥0),则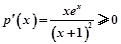 ,
,
∴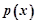 在
在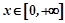 单调递增,
单调递增,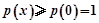 (x=1时取等号),
(x=1时取等号),
∴t≤1 4分.
(2)设x1、x2是任意的两实数,且x1<x2,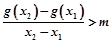 ,故
,故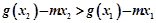 ,
,
设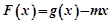 ,则F(x)在R上单增,(7分)
,则F(x)在R上单增,(7分)
即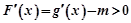 恒成立.
恒成立.
即对任意的t≤-1,x∈R,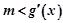 恒成立.
恒成立.
而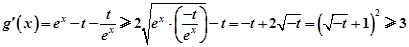
故m<3.(9分)
(3)由(1)知,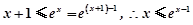
取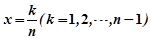 ,则
,则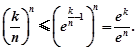
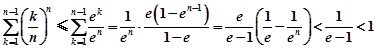
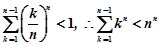
∴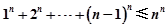 (n∈N*).(14分)
(n∈N*).(14分)
考点:导数法,分离变量法,放缩法证明不等式.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 (
( )
) 的单调性;
的单调性; 处取得极值,不等式
处取得极值,不等式 对任意
对任意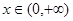 恒成立,求实数
恒成立,求实数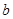 的取值范围;
的取值范围;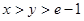 时,证明不等式
时,证明不等式 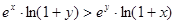 .
.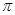 为圆周率,
为圆周率,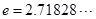 为自然对数的底数.
为自然对数的底数.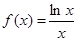 的单调区间;
的单调区间;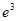 ,
,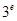 ,
,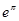 ,
,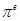 ,
, ,
,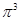 这6个数中的最大数与最小数;
这6个数中的最大数与最小数;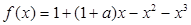 ,其中
,其中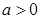 .
. 在其定义域上的单调性;
在其定义域上的单调性;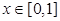 时,求
时,求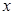 的值.
的值. .
.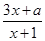 在区间[3,10]上封闭,求实数a的取值范围;
在区间[3,10]上封闭,求实数a的取值范围;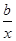 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.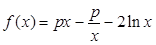 .
.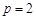 ,求曲线
,求曲线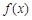 在点
在点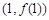 处的切线方程;
处的切线方程;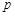 的取值范围;
的取值范围;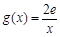 ,若在
,若在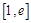 上至少存在一点
上至少存在一点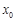 ,使得
,使得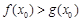 成立,求实数
成立,求实数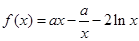 .
. 在
在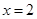 时有极值,求实数
时有极值,求实数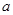 的值和
的值和