题目内容
7.若向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=3,则|$\overrightarrow{a}$|•|$\overrightarrow{b}$|的取值范围是[$\frac{5}{4}$,$\frac{13}{4}$].分析 设向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为θ,由数量积的计算公式可得$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{4}{5}$,分析可得180°≥θ>90°,
由-1≤cosθ<0,且$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=-$\frac{4}{5}$,得出|$\overrightarrow{a}$|•|$\overrightarrow{b}$|的取值范围.
解答 解:设向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为θ,
对于向量$\overrightarrow{a}$、$\overrightarrow{b}$有:|$\overrightarrow{a}$+$\overrightarrow{b}$|=2①,|$\overrightarrow{a}$-$\overrightarrow{b}$|=3②,
①2-②2可得:4$\overrightarrow{a}$•$\overrightarrow{b}$=-5,即$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{5}{4}$,
且向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角θ满足0°≤θ≤180°,
∴有-1≤cosθ≤1,
由$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=-$\frac{5}{4}$,
∴|$\overrightarrow{a}$|•|$\overrightarrow{b}$|=$\frac{-\frac{5}{4}}{cosθ}$,
∵|$\overrightarrow{a}$|•|$\overrightarrow{b}$|≥0,∴-1≤cosθ<0,
∴|$\overrightarrow{a}$|•|$\overrightarrow{b}$|≥$\frac{5}{4}$;
又①2+②2得:2${\overrightarrow{a}}^{2}$+2${\overrightarrow{b}}^{2}$=13,
∴${|\overrightarrow{a}|}^{2}$+${|\overrightarrow{b}|}^{2}$=$\frac{13}{2}$,
且${|\overrightarrow{a}|}^{2}$+${|\overrightarrow{b}|}^{2}$≥2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,
∴|$\overrightarrow{a}$|•|$\overrightarrow{b}$|≤$\frac{13}{4}$;
综上,$\frac{5}{4}$≤|$\overrightarrow{a}$|•|$\overrightarrow{b}$|≤$\frac{13}{4}$.
故答案为:[$\frac{5}{4}$,$\frac{13}{4}$].
点评 本题考查了平面向量数量积的运算问题,掌握数量积与夹角公式是解题的关键.

| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
| A. | 4 | B. | 4$\sqrt{2}$ | C. | 8 | D. | 8$\sqrt{2}$ |
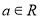 ,则“
,则“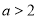 ”是“
”是“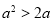 ”的( )
”的( ) 在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,E为PA的中点.
在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,E为PA的中点.