题目内容
12.某校640名毕业生学生,现采用系统抽样方法,抽取32人做问卷调查,将640人按1,2,…,640随机编号,则抽取的32人中,编号落入区间[161,380]的人数为( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
分析 根据系统抽样方法,从640人中抽取32人,即从20人抽取1人.从而得出从编号161~380共220人中抽取的人数即可.
解答 解:使用系统抽样方法,从640人中抽取32人,即从20人抽取1人.
∴从编号161~380共220人中抽取$\frac{220}{20}$=11人.
故选:B.
点评 本题主要考查系统抽样的定义和方法,属于基础题.

练习册系列答案
相关题目
3.已知定义在实数集R上的函数f(x)满足f(x+1)=$\frac{1}{2}$+$\sqrt{f(x)-{f}^{2}(x)}$,则f(0)+f(2017)的最大值为( )
| A. | 1-$\frac{\sqrt{2}}{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
20.若函数f(x)=a(x-2)ex+lnx+$\frac{1}{x}$存在唯一的极值点,且此极值大于0,则( )
| A. | 0≤a<$\frac{1}{e}$ | B. | 0≤a<$\frac{1}{{e}^{2}}$ | C. | -$\frac{1}{e}$<a<$\frac{1}{{e}^{2}}$ | D. | 0≤a<$\frac{1}{e}$或a=-$\frac{1}{e}$ |
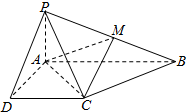 已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$,AB=1,M是PB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$,AB=1,M是PB的中点.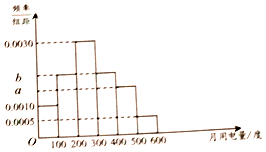 某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.