题目内容

9．若f（x）=$\frac{{e}^{x}-{e}^{-x}}{2}$，g（x）=$\frac{{e}^{x}+{e}^{-x}}{2}$，则f（2x）等于（　　）
A．2f（x）B．2[f（x）+g（x）]C．2g（x）D．2f（x）•g（x）

分析 f（2x）=$\frac{{e}^{2x}-{e}^{-2x}}{2}$=$\frac{（{e}^{x}-{e}^{-x}）（{e}^{x}+{e}^{-x}）}{2}$，即可得出．

解答 解：f（2x）=$\frac{{e}^{2x}-{e}^{-2x}}{2}$=$\frac{（{e}^{x}-{e}^{-x}）（{e}^{x}+{e}^{-x}）}{2}$=2f（x）g（x）．
故选：D．

点评 本题考查了指数运算性质、乘法公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
19．双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为2，焦点到渐近线的距离为2$\sqrt{3}$．
20．设a=tan$\frac{3}{4}$π，b=cos$\frac{π}{4}$，c=（1+sin$\frac{6}{5}$π）0，则a，b，c的大小关系是（　　）
A．c＞b＞aB．c＞a＞bC．a＞b＞cD．b＞c＞a
17．某移动公司对[25，55]岁的人群随机抽取n人进行了一次是否愿意使用4G网络的社会调查，若愿意使用的称为“4G族”，否则称为“非4G族”，得如下统计表和各年龄段人数频率分布直方图：

（1）补全频率分布直方图并求n、a的值；
（2）用频率分布直方图估计“4G族”年龄的中位数，和平均数（不用写过程只写数据）；
（3）从年龄段在[40，50）的“4G族”中采用分层抽样法抽取6人参加4G网络体验活动，求年龄段分别在[40，45）、[45，50）中抽取的人数．
4．已知向量$\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（5，-3），则$\overrightarrow{a}$•$\overrightarrow{b}$的值为（　　）
A．-1B．7C．13D．11
14．若a2+b2=1，x2+y2=4，则ax+by的最大值为2．
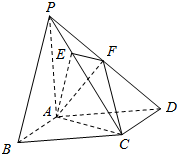1．如图，四棱锥P-ABCD的底面ABCD是正方形，PA⊥平面ABCD，AP=AD=1，点E在PC上，且PE=$\frac{1}{2}$EC，点F是PD的中点．
（1）求证：PC⊥AF；
（2）求三棱锥A-CEF的体积．
18．在平面几何里，“若CD是Rt△ABC的斜边AB上的高，则$\frac{1}{{C{D^2}}}=\frac{1}{{C{A^2}}}+\frac{1}{{C{B^2}}}$．”拓展到空间，研究三棱锥的高与侧棱间的关系，可得出的正确结论是：“若三棱锥A-BCD的三侧面ABC、ACD、ADB两两互相垂直，AO是三棱锥A-BCD的高，则$\frac{1}{{A{O^2}}}=\frac{1}{{A{B^2}}}+\frac{1}{{A{C^2}}}+\frac{1}{{A{D^2}}}$”．
19．设函数f（x）=|2x-1|，x∈R．
（Ⅰ）求不等式|f（x）-2|≤5的解集；
（Ⅱ）若g（x）=$\frac{1}{f（x）+f（x-1）+m}$的定义域为R，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网