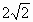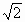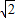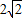Question

已知斜率为k的直线y=kx被圆x²+y²=2所截，截得的弦AB的长等于（　　）

• A、4
• B、2
• C、

  2

• D、2

  2

Answer 1

分析：通过观察，可知，直线y=kx过原点，而圆x²+y²=2的圆心就是原点，所以直线y=kx过圆x²+y²=2的圆心，所以弦AB就是圆直径，弦AB的长可求．

解答：解：由题意知，直线y=kx过圆x²+y²=2的圆心，∴弦AB为圆直径，∵圆半径为

2

，∴直径为2

2

故选D

点评：本题考查了圆中弦长的求法，做题时注意结合图象．