题目内容
设f(x)=ex-ax+
,x∈R,已知斜率为k的直线与y=f(x)的图象交于A(x1,y1),B(x2,y2)(x1≠x2)两点,若对任意的a<-2,k>m恒成立,则m的最大值为( )
| a |
| ex |
A、-2+
| ||
| B、0 | ||
C、2+
| ||
D、2+2
|
分析:可考虑斜率为k的直线与y=f(x)的图象相切的情况,设出切点,求出相切时k的最小值,由不等式恒成立结论:a<f(x)恒成立?a<f(x)min得到m的最大值.
解答:解:因为f(x)=ex-ax+
,
所以导数f'(x)=ex-a-
当斜率为k的直线与y=f(x)的图象相切,设切点(x0,y0),
则k=ex0-a-
=ex0+
-a,
由于a<-2,
所以-a>2,k≥2
+(-a),
即k≥(
+1)2-1>(
+1)2-1,
即k>2+2
.
因为对任意的a<-2,k>m恒成立,
所以m≤k的最小值,即m≤2+2
.
故选D.
| a |
| ex |
所以导数f'(x)=ex-a-
| a |
| ex |
当斜率为k的直线与y=f(x)的图象相切,设切点(x0,y0),
则k=ex0-a-
| a |
| ex0 |
| -a |
| ex0 |
由于a<-2,
所以-a>2,k≥2
| -a |
即k≥(
| -a |
| 2 |
即k>2+2
| 2 |
因为对任意的a<-2,k>m恒成立,
所以m≤k的最小值,即m≤2+2
| 2 |
故选D.
点评:本题考查了函数恒成立问题,结合图象观察直线与曲线相切求出斜率的范围,根据恒成立转化为求最值,应用基本不等式和二次函数的知识,求出k的范围,得出结论.本题属于难题.

练习册系列答案
相关题目
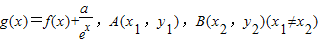 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;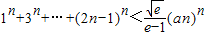 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由. 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;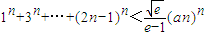 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.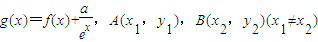 是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围;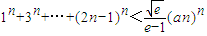 对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.
对一切正整数n都成立?若存在,求a的最小值;若不存在,请说明理由.