题目内容
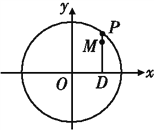
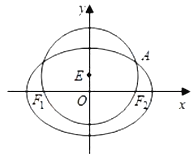
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)求椭圆标准方程,由圆与![]() 轴的交点,可求得
轴的交点,可求得![]() ,利用
,利用![]() 三点共线,由
三点共线,由![]() 是圆的直径,从而
是圆的直径,从而![]() ,利用勾股定理可求得
,利用勾股定理可求得![]() ,从而由椭圆的定义可求得
,从而由椭圆的定义可求得![]() ,于是得
,于是得![]() ,椭圆方程即得;
,椭圆方程即得;
(2)![]() 是确定的,
是确定的, ![]() ,说明
,说明![]() ,于是直线
,于是直线![]() 斜率已知,设出其方程为
斜率已知,设出其方程为![]() ,代入椭圆方程,消去
,代入椭圆方程,消去![]() 得
得![]() 的二次方程,从而有
的二次方程,从而有![]() (
(![]() 分别是
分别是![]() 的横坐标),由直线与圆锥曲线相交的弦长公式可求得弦长
的横坐标),由直线与圆锥曲线相交的弦长公式可求得弦长![]() ,再由点到直线距离公式求出
,再由点到直线距离公式求出![]() 到直线
到直线![]() 的距离,可计算出
的距离,可计算出![]() 的面积,最后利用基本不等式可求得面积的最大值,及此时的
的面积,最后利用基本不等式可求得面积的最大值,及此时的![]() 值,得直线方程.
值,得直线方程.
解析:
(1)
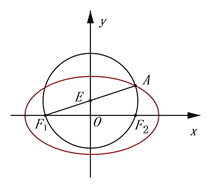
如图,圆![]() 经过椭圆
经过椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() ,所以
,所以![]() ,解得
,解得![]() ,因为
,因为![]() ,
, ![]() ,
,![]() 三点共线,所以
三点共线,所以![]() 为圆
为圆![]() 的直径, 所以
的直径, 所以![]() ,因为
,因为![]() ,所以
,所以![]() .所以
.所以![]() ,由
,由![]() ,得
,得![]() .所以椭圆
.所以椭圆![]() 的方程为
的方程为![]() .
.
(2)由(1)得,点![]() 的坐标为
的坐标为![]() ,因为
,因为![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立
,联立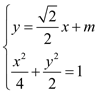 ,得
,得![]() ,设
,设![]() ,由
,由![]() ,得
,得![]() .因为
.因为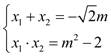
所以![]() , 又点
, 又点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]()
![]() .当且仅当
.当且仅当![]() ,即
,即![]() 时,等号成立,所以直线
时,等号成立,所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目