题目内容
4．某城市在发展过程中，交通状况逐渐受到大家更多的关注，据有关统计数据显示，从6时到9时，车辆通过某市某一路段的用时y（min）与车辆进入该路段的时刻t之间的关系可近似地用函数表示为：y=-$\frac{1}{8}$t3-$\frac{3}{4}$t2+36t-$\frac{629}{4}$，则在这段时间内，通过路段用时最多的时刻是（ ）| A． | 6时 | B． | 7时 | C． | 8时 | D． | 9时 |
分析 求导并化简y′=-$\frac{3}{8}$t2-$\frac{3}{2}$t+36=-$\frac{3}{8}$（t-8）（t+12），从而确定函数的单调性及最值点即可．
解答 解：∵y=-$\frac{1}{8}$t3-$\frac{3}{4}$t2+36t-$\frac{629}{4}$，
∴y′=-$\frac{3}{8}$t2-$\frac{3}{2}$t+36
=-$\frac{3}{8}$（t2+4t-12×8）
=-$\frac{3}{8}$（t-8）（t+12），
故函数y=-$\frac{1}{8}$t3-$\frac{3}{4}$t2+36t-$\frac{629}{4}$在（0，8）上是增函数，
在（8，24）上减函数；
故当t=8时，y有最大值，
故通过路段用时最多的时刻是8时，
故选C．
点评 本题考查了导数的综合应用及函数的单调性与最值的判断与求法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．已知实数a，b满足$\left\{{\begin{array}{l}{0＜a＜2}\\{0＜b＜2}\end{array}}\right.$，则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$表示焦点在x轴上且离心率小于$\frac{{\sqrt{3}}}{2}$的椭圆的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |
15．已知函数f（x）=$\frac{x}{x+1}$+2x-mln（x+1）在（-1，+∞）上是增函数，则实数m的取值范围为（ ）
| A． | （-∞，2$\sqrt{2}$] | B． | （-∞，2$\sqrt{2}$） | C． | （-∞，3） | D． | （-∞，3] |
9．以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角性”．
该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数为（ ）
该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数为（ ）
| A． | 2017×22015 | B． | 2017×22014 | C． | 2016×22015 | D． | 2016×22014 |
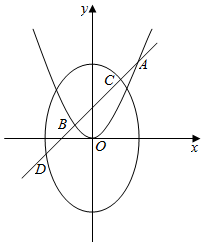如图，抛物线C1：y=$\frac{1}{4}$x2的焦点F也是椭圆C2：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点，且在两曲线的一个公共点处的直线l1：$\sqrt{6}$x-2y-3=0与C1相切．
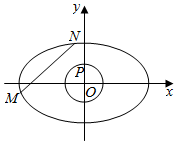如图，已知椭圆C：$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1，圆O：x2+y2=1，其中M，N是椭圆C上的两个动点，P是圆O上一个动点．