题目内容
(本小题满分16分)已知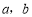 为实数,函数
为实数,函数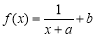 ,函数
,函数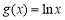 .
.
(1)当 时,令
时,令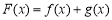 ,求函数
,求函数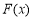 的极值;
的极值;
(2)当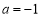 时,令
时,令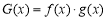 ,是否存在实数
,是否存在实数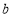 ,使得对于函数
,使得对于函数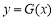 定义域中的任意实数
定义域中的任意实数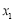 ,均存在实数
,均存在实数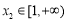 ,有
,有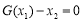 成立,若存在,求出实数
成立,若存在,求出实数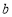 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
(1)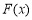 的极小值为
的极小值为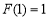 ,无极大值.(2)
,无极大值.(2)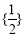
【解析】
试题分析:(1)当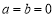 时,
时,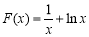 ,定义域为
,定义域为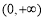 ,由
,由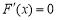 得
得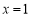 .列表分析得
.列表分析得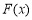 的极小值为
的极小值为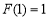 ,无极大值.(2)恒成立问题及存在问题,一般利用最值进行转化:
,无极大值.(2)恒成立问题及存在问题,一般利用最值进行转化: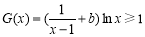 在
在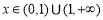 上恒成立.由于
上恒成立.由于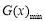 不易求,因此再进行转化:当
不易求,因此再进行转化:当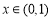 时,
时, 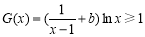 可化为
可化为 ,令
,令 ,问题转化为:
,问题转化为: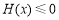 对任意
对任意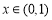 恒成立;同理当
恒成立;同理当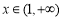 时,
时,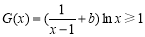 可化为
可化为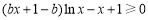 ,令
,令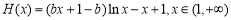 ,问题转化为:
,问题转化为: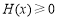 对任意的
对任意的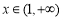 恒成立;以下根据导函数零点情况进行讨论即可.
恒成立;以下根据导函数零点情况进行讨论即可.
试题解析:(1)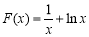 ,
,
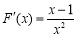 ,令
,令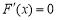 ,得
,得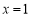 . 1分
. 1分
列表:
x |
|
|
|
|
| 0 | + |
| ↘ | 极小值 | ↗ |
所以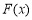 的极小值为
的极小值为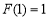 ,无极大值. 4分
,无极大值. 4分
(2)当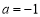 时,假设存在实数
时,假设存在实数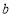 满足条件,则
满足条件,则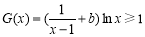 在
在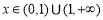 上恒成立. 5分
上恒成立. 5分
1)当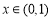 时,
时, 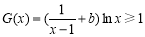 可化为
可化为 ,
,
令 ,问题转化为:
,问题转化为: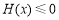 对任意
对任意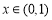 恒成立;(*)
恒成立;(*)
则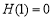 ,
,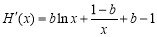 ,
,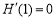 .
.
令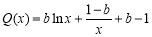 ,则
,则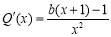 .
.
①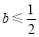 时,因为
时,因为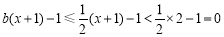 ,
,
故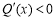 ,所以函数
,所以函数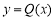 在
在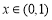 时单调递减,
时单调递减,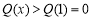 ,
,
即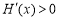 ,从而函数
,从而函数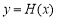 在
在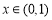 时单调递增,故
时单调递增,故 ,所以(*)
,所以(*)
成立,满足题意; 7分
②当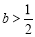 时,
时,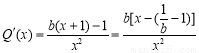 ,
,
因为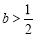 ,所以
,所以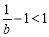 ,记
,记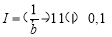 ,则当
,则当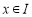 时,
时,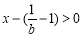 ,
,
故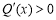 ,所以函数
,所以函数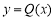 在
在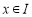 时单调递增,
时单调递增,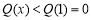 ,
,
即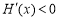 ,从而函数
,从而函数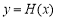 在
在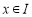 时单调递减,所以
时单调递减,所以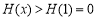 ,此时(*)不成立;
,此时(*)不成立;
所以当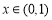 ,
, 恒成立时,
恒成立时,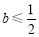 ; 9分
; 9分
2)当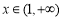 时,
时,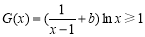 可化为
可化为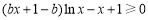 ,
,
令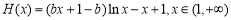 ,问题转化为:
,问题转化为: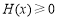 对任意的
对任意的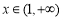 恒成立;(**)
恒成立;(**)
则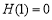 ,
,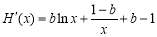 ,
,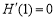 .
.
令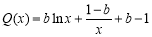 ,则
,则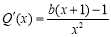 .
.
①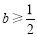 时,
时,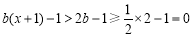 ,
,
故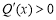 ,所以函数
,所以函数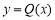 在
在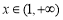 时单调递增,
时单调递增,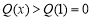 ,
,
即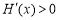 ,从而函数
,从而函数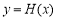 在
在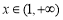 时单调递增,所以
时单调递增,所以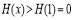 ,此时(**)成立;11分
,此时(**)成立;11分
②当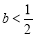 时,
时,
ⅰ)若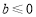 ,必有
,必有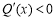 ,故函数
,故函数 在
在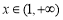 上单调递减,所以
上单调递减,所以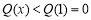 ,即
,即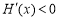 ,从而函数
,从而函数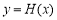 在
在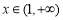 时单调递减,所以
时单调递减,所以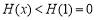 ,此时(**)不成立; 13分
,此时(**)不成立; 13分
ⅱ)若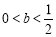 ,则
,则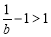 ,所以当
,所以当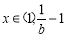 时,
时,
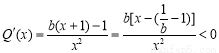 ,
,
故函数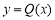 在
在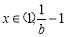 上单调递减,
上单调递减,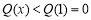 ,即
,即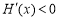 ,所以函数
,所以函数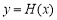 在
在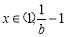 时单调递减,所以
时单调递减,所以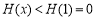 ,此时(**)不成立;
,此时(**)不成立;
所以当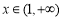 ,
,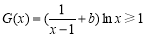 恒成立时,
恒成立时, ; 15分
; 15分
综上所述,当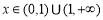 ,
,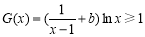 恒成立时,
恒成立时, 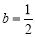 ,从而实数
,从而实数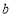 的取值集合为
的取值集合为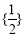 . 16分
. 16分
考点:利用导数求极值,利用导数研究函数单调性
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:








 是奇函数,则
是奇函数,则 .
.
 若函数
若函数 恰有三个不同的零点,则实数
恰有三个不同的零点,则实数 的取值范围是 .
的取值范围是 . 中,
中, ,若前5项的和
,若前5项的和 ,则其公差为 .
,则其公差为 .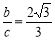 ,
, .
. 的值;(2)求
的值;(2)求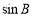 的值;(3)若
的值;(3)若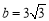 ,求△ABC的面积.
,求△ABC的面积. 满足约束条件
满足约束条件 则目标函数
则目标函数 的最小值为 .
的最小值为 .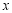 (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为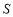 (m2).
(m2).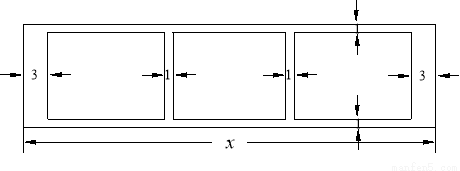
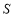 关于
关于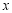 的函数关系式;
的函数关系式;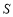 的最大值.
的最大值.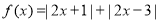 .
. 的解集;
的解集;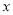 的不等式
的不等式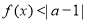 的解集非空,求实数
的解集非空,求实数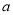 的取值范围.
的取值范围.