题目内容
如图2-5-14,P为圆O外一点,PA、PB是圆O的两条切线,A、B为切点,OP与AB相交于点M,且点C是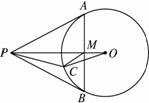
上一点.求证:∠OPC =∠OCM.
图2-5-14
思路分析:图形中有两条切线,故运用切割线定理得线段和角的关系,在Rt△OPB中运用射影定理,有OB2=OP·OM,代换其中的OB为OC,可得三角形相似,即得角的相等关系.
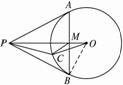
证明:连结OB,由切线长定理,得PA =PB,PM⊥AB,PO平分∠APB.?
又PB⊥OB,在Rt△OPB中,OB2=OP·OM,?
∵OB=OC,?
∴OC2=OP·OM,
即
=
.?
∴△OCP∽△OMC.∴∠OPC =∠OCM.
练习册系列答案
名校课堂系列答案
相关题目
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数P与听课时间t之间的关系满足如图所示的曲线．当t∈（0，14]时，曲线是二次函数图象的一部分，当t∈[14，40]时，曲线是函数y=logα（x-5）+83（a＞0且a≠1）图象的一部分．根据专家研究，当注意力指数P大于等于80时听课效果最佳．
（2011•盐城二模）如图，在平面直角坐标系xOy中，已知曲线C由圆弧C1和圆弧C2相接而成．两相接点M，N均在直线x=5上，圆弧C1的圆心是坐标原点O，半径为r1=13； 圆弧C2过点A（29，0）．
=
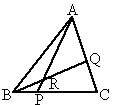
分别是PB,CD上的点,且
,过点E作BC的平行线交PC于G.
时,求△EFG的面积。